
分析 ( I)求出抛物线的$F({\frac{p}{2},0})$.利用$|{FP}|=3+\frac{p}{2}=|{FS}|$,则S(3+p,0),通过|PF|=|PS|,解得p=2.得到抛物线C的方程.
( II)( i)由( I)知F(1,0),设P(x0,y0),(x0y0≠0),S(xS,0)(xS>0),求出S(x0+2,0).得到直线PQ的斜率KPQ=$-\frac{{y}_{0}}{2}$.利用直线l1和直线PQ平行,设直线l1的方程为$y=-\frac{y_0}{2}x+b$,代入抛物线方程,求出$b=-\frac{2}{y_0}$.设E(xE,yE),求出kPE=$\frac{{y}_{E}-{y}_{0}}{{x}_{E}-{x}_{0}}$=$\frac{{y}_{0}}{{x}_{0}-1}$,可得直线PE的方程,表示出△OPE的面积,利用基本不等式求解三角形OPE的面积的最小值.
( ii)由( i)知$y_0^2≠4$时,直线PE的方程$y-{y_0}=\frac{y_0}{{{x_0}-1}}({x-{x_0}})$,整理可得$y=\frac{{4{y_0}}}{y_0^2-4}({x-1})$,然后求解过点F(1,0).
解答 解:( I)由题意知$F({\frac{p}{2},0})$.xP=3,则$|{FP}|=3+\frac{p}{2}=|{FS}|$,
则S(3+p,0),或S(-3,0)(舍)则FS中点$({\frac{3p+6}{4},0})$.
因为|PF|=|PS|,则$\frac{3p+6}{4}=3$解得p=2.所以抛物线C的方程为y2=4x.…..(4分)
( II)( i)由( I)知F(1,0),设P(x0,y0),(x0y0≠0),S(xS,0)(xS>0),
因为|FP|=|FS|,则|xS-1|=x0+1,由xS>0得xS=x0+2,故S(x0+2,0).故直线PQ的斜率KPQ=$-\frac{{y}_{0}}{2}$.
因为直线l1和直线PQ平行,设直线l1的方程为$y=-\frac{y_0}{2}x+b$,代入抛物线方程
得${y^2}+\frac{8}{y_0}y-\frac{8b}{y_0}=0$,由题意$△=\frac{64}{y_0^2}+\frac{32b}{y_0}=0$,得$b=-\frac{2}{y_0}$.
设E(xE,yE),则yk=-$\frac{4}{{y}_{0}}$,xK=$\frac{4}{{{y}_{0}}^{2}}$=$\frac{1}{{x}_{0}}$,
当y02≠4时,kPE=$\frac{{y}_{E}-{y}_{0}}{{x}_{E}-{x}_{0}}$=$\frac{{y}_{0}}{{x}_{0}-1}$,
可得直线PE的方程为$y-{y_0}=\frac{y_0}{{{x_0}-1}}({x-{x_0}})$,
则O到直线PE的距离为$d=\frac{{|{\frac{{{x_0}{y_0}}}{{{x_0}-1}}-{y_0}}|}}{{\sqrt{1+{{(\frac{y_0}{{{x_0}-1}})}^2}}}}=\frac{{|{y_0}|}}{{{x_0}+1}}$,
$|{PE}|=\sqrt{{{({x_0}-\frac{1}{x_0})}^2}+{{({y_0}+\frac{4}{y_0})}^2}}=\frac{{{{({x_0}+1)}^2}}}{x_0}$…..(6分)
所以,△OPE的面积${S_{△OPE}}=\frac{1}{2}|{PE}|×d=\frac{{|{y_0}|({x_0}+1)}}{x_0}=\frac{(y_0^2+4)}{{|{y_0}|}}=|{y_0}|+\frac{4}{{|{y_0}|}}>2$
当$y_0^2=4$时,S△OPE=2
所以,△OPE的面积有最小值,最小值为2.…..(9分)
( ii)由( i)知$y_0^2≠4$时,直线PE的方程$y-{y_0}=\frac{y_0}{{{x_0}-1}}({x-{x_0}})$,
整理可得$y=\frac{{4{y_0}}}{y_0^2-4}({x-1})$,直线PE恒过点F(1,0).
当$y_0^2=4$时,直线PE的方程为x=1,过点F(1,0).…..(12分)
点评 本题考查抛物线方程的求法,直线与抛物线的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{2}$ | B. | $\frac{3\sqrt{11}}{11}$ | C. | $\frac{{\sqrt{19}}}{19}$ | D. | $\frac{{3\sqrt{19}}}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
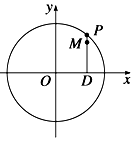 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m?α,n?α,m∥β,l∥β,则α∥β | ||
| C. | 若α⊥β,m?α,则m⊥β | D. | 若α⊥β,m⊥β,m?α,则m∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
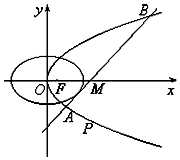 如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.
如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}})$ | B. | $({-1,\frac{1}{2}})$ | C. | $({0,\frac{1}{2}})$ | D. | (-∞,-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com