
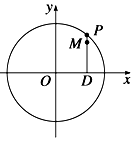
 ��ͼ����P��Բx2+y2=6�ϵĶ��㣬��D��P��x���ϵ�ͶӰ��MΪPD��һ�㣬��$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$��
��ͼ����P��Բx2+y2=6�ϵĶ��㣬��D��P��x���ϵ�ͶӰ��MΪPD��һ�㣬��$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$������ ��1����M������Ϊ��x��y��������֪�õ�P�������ǣ�x��$\sqrt{2}$y�����ɴ������M�Ĺ켣C�ķ��̣�
��2��ֱ��l������C�ཻ��ΪABA��x1��y1����B��x2��y2����������ʽ������������е����깫ʽ��б�ʼ��㹫ʽ���ɵó���
��3�����|FH|�����ֵ���������SEFGH�����ֵ��
��� �⣺��1����$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$֪��MΪ�߶�PD���е㣬
���M�������ǣ�x��y�������P�������ǣ�x��$\sqrt{2}$y����
�ߵ�P��Բx2+y2=6�ϣ�
��x2+2y2=6������3�֣�
������C�ķ���Ϊ$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1��
��2��ֱ��l������C�ཻ��ΪAB��A��x1��y1����B��x2��y2����
������Բ���̣���ʽ����ɵã���x1+x2����x1-x2��+2��y1+y2����y1-y2��=0��
����AB�е�Ϊ��1��1����
��kAB=-$\frac{1}{2}$��
��ֱ��l�ķ���Ϊy-1=-$\frac{1}{2}$��x-1�������x+2y-3=0��
��3����FH�ķ���Ϊy=x+b��������Բ���̣��ɵ�3x2+4bx+2b2-6=0��
��|FH|=$\sqrt{2}•\sqrt{��-\frac{4b}{3}��^{2}-4•\frac{2{b}^{2}-6}{3}}$=$\sqrt{2}$•$\sqrt{-\frac{8}{9}{b}^{2}+8}$��
��b=0��|FH|�����ֵΪ4��
ֱ��$x+y-\sqrt{3}=0$������C�������ɵ�$3{x}^{2}-4\sqrt{3}x=0$��
��|EG|=$\sqrt{2}•\frac{4\sqrt{3}}{3}$=$\frac{4\sqrt{6}}{3}$��
��SEFGH�����ֵΪ$\frac{8\sqrt{6}}{3}$��
���� ���⿼��켣���̣���������Բ�ı����̼������ʡ����������е����깫ʽ��б�ʼ��㹫ʽ��������������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y=sin��{\frac{x}{2}+\frac{5��}{6}}��$ | B�� | $y=sin��{2x-\frac{��}{6}}��$ | C�� | y=2sin2x-1 | D�� | $y=cos��{2x-\frac{��}{6}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2ln 2 | B�� | 2-ln 2 | C�� | 4-ln 2 | D�� | 4-2ln 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
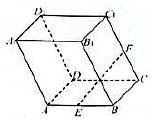 ��ͼ��ʾ����ƽ��������ABCD-A1B1C1D1�У������DZ߳�Ϊ2�������Σ�����AA1�ij�Ϊ2���ҡ�A1AB=��A1AD=120�㣬EΪAB���е㣬FΪCC1���е㣬��EF�ij�Ϊ$\sqrt{3}$��
��ͼ��ʾ����ƽ��������ABCD-A1B1C1D1�У������DZ߳�Ϊ2�������Σ�����AA1�ij�Ϊ2���ҡ�A1AB=��A1AD=120�㣬EΪAB���е㣬FΪCC1���е㣬��EF�ij�Ϊ$\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com