
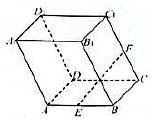
 如图所示,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,则EF的长为$\sqrt{3}$.
如图所示,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,则EF的长为$\sqrt{3}$. 分析 利用向量模的计算公式和向量的数量积的定义即可得出.
解答 解:∵$\overrightarrow{EF}$=$\overrightarrow{EB}$+$\overrightarrow{BC}$+$\overrightarrow{CF}$,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,
∴${\overrightarrow{EF}}^{2}$=1+4+1+2•1•2•cos90°+2•2•1•cos120°+2•1•1•cos120°=3,
∴$\overrightarrow{EF}$=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 熟练掌握向量模的计算公式和向量的数量积的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
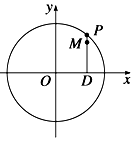 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为PD上一点,且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
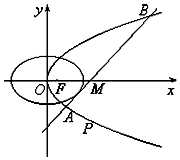 如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.
如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点O,过点,M(4,0)的直线l与抛物线C2分别相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}})$ | B. | $({-1,\frac{1}{2}})$ | C. | $({0,\frac{1}{2}})$ | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
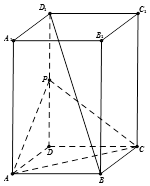 .如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
.如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com