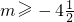解:(1)∵点(S
n,S
n+1)在直线y=kx+1上,
故S
n+1=kS
n+1.
n=1时,a
1+a
2=ka
1+1
又a
1=1,a
2=2,则1+2=k+1,∴k=2;
(2)由(1)知S
n+1=2S
n+1①
当n≥2时,S
n=2S
n-1+1②
①-②得a
n+1=2a
n(n≥2)
又a
2=2a
1,易见a
n≠0(n∈N
+),∴

=2(n∈N
+)
故{a
n}成等比数列.
∴a
n=1×2
n-1=2
n-1.
(3)∵
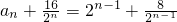
在n≥3时,单调递增
在1≤n≤2时,单调递减
∴当n=2或3时,
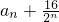
有最小值为
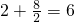
又不等式
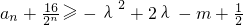
,对一切n∈N*恒成立.
∴
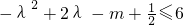
,

对一切λ∈R恒成立.
∴
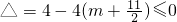
,
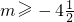
∴整数m的最小值为-4.
分析:(1)根据点在直线上,把点的坐标代入直线方程,得到两者之间的关系,给出当n=1时的结果,用待定系数法求出变量的值.
(2)根据所给的前n项和之间的关系,仿写一个关系式,两式相减得到通项之间的关系,从而得到数列是等比数列,注意验证首相是否符合.
(3)构造新的函数,注意函数的单调性,特殊项进行验证,把函数式进行整理,变为函数的恒成立问题,二次函数大于零恒成立,问题转换为二次函数的最值问题,利用判别式解决.
点评:数列中数的有序性是数列定义的灵魂,要注意辨析数列中的项与数集中元素的异同 因此在研究数列问题时既要注意函数方法的普遍性,又要注意数列方法的特殊性.

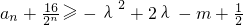 对一切正整数n和实数λ均恒成立,求整数m的最小值.
对一切正整数n和实数λ均恒成立,求整数m的最小值. =2(n∈N+)
=2(n∈N+)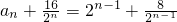
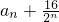 有最小值为
有最小值为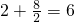
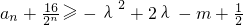 ,对一切n∈N*恒成立.
,对一切n∈N*恒成立.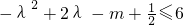 ,
, 对一切λ∈R恒成立.
对一切λ∈R恒成立.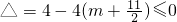 ,
,