练习册

  • 练习册
  • 试题
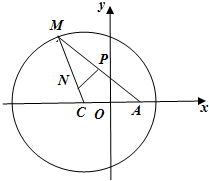    精英家教网 > 高中数学 > 题目详情
    如图，过点（1，0）的直线l与中心在原点，焦点在x轴上且离心率为的椭圆相交于A、B两点，直线过线段AB的中点M，同时椭圆上存在一点与右焦点F关于直线l对称，求直线l和椭圆的方程.

     

    答案：
    解析：

    		答案：解：由题意，  ∴椭圆方程可设为：

        设直线l：y=k(x－1)，显然k≠0，将直线方程代入椭圆方程：

        

         整理得：  ①

         设交点A（x1,y1），B（x2,y2），中点M（x0,y0），而中点在直线上，

         ∴  ∴，

         求得：k=－1，将k=－1代入①，其中△>0求得，点

    F（c，0）关于直线l：y=－x+1的对称点（1，1－c）在椭圆上，代入椭圆方程：

    ∴1+2(1－c)2－2c2=0， ∴

    ∴所求椭圆为C：，直线l方程为：

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网已知圆C：（x+1）2+y2=8．
    （1）求过点Q（3，0）的圆C的切线l的方程；
    （2）如图，定点A（1，0），M为圆C上一动点，点P在AM上，点N在CM上，且满足
    AM
    =2
    AP
    ，
    NP
    •
    AM
    =0    ，求点N的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源：高中数学综合题 题型：044

    图，过点A(-1，0)，斜率为k的直线l与抛物线C：交于P、Q两点．

    (1)若曲线C的焦点F与P，Q，R三点按如图顺序构成平行四边形PFQR，求点R的轨迹方程；

    (2)设P，Q两点只在第一象限运动，(0，8)点与线段PQ中点的连线交x轴于点N，当点N在A点右侧时，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2007届潜山中学理复(一、二)数学周考试卷 题型：044

    解答题

    如图：过点A1(1，0)作y轴平行线与曲线C：y＝x2(＞0，x＞0)交于B1点，过B1作曲线C的切线交x轴于A2，再过A2作y轴平行线交曲线C于B2，过B2作曲线C的切线交x轴于A3……，如此继续无限下去，得到点列:{An(an，0)}、{Bn(an，bn)}，设△AnBnAn＋1的面积为Sn．

    (1)

    求数列{an}的通项公式．

    (2)

    若设cn＝log2Sn，且{cn}的前n项和Tn中，只有T2最大，求的范围．

    (3)

    若设Tn＝S1＋S2＋…＋Sn，且数列{cn}、{Tn}满足＝1，c1＝

    8cn＝Tn－1＋cn－1求{cn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

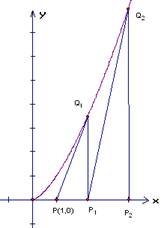
    （08年咸阳市一模） （14分）如图，过点P(1,0)作曲线C: 的切线，切点为,设点在x轴上的投影是点；又过点作曲线C的切线，切点为,设在x轴上的投影是；…；依此下去,得到一系列点,,…,,…,设点的横坐标为.

    （Ⅰ）试求数列｛｝的通项公式；（用的代数式表示）

    （Ⅱ）求证：

    （Ⅲ）求证：（注：）.

     

    查看答案和解析>>

    同步练习册答案