
| A. | (1,4] | B. | (2,4] | C. | (2,4) | D. | (2,+∞) |
分析 根据f(x)=$\left\{\begin{array}{l}{(a-2)x-1,x≤1}\\{a+\frac{1{-a}^{2}}{x+a},x>1}\end{array}\right.$ 在(-∞,+∞)上单调递增,可得 $\left\{\begin{array}{l}{a-2>0}\\{1{-a}^{2}<0}\\{a-2-1≤\frac{a+1}{1+a}}\end{array}\right.$,由此求得实数a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{(a-2)x-1,x≤1}\\{\frac{ax+1}{x+a},x>1}\end{array}\right.$=$\left\{\begin{array}{l}{(a-2)x-1,x≤1}\\{a+\frac{1{-a}^{2}}{x+a},x>1}\end{array}\right.$ 在(-∞,+∞)上单调递增,∴$\left\{\begin{array}{l}{a-2>0}\\{1{-a}^{2}<0}\\{a-2-1≤\frac{a+1}{1+a}}\end{array}\right.$,
求得2<a≤4,
故选:B.
点评 本题主要考查函数的单调性的性质,属于基础题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
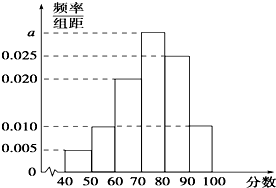 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a为正相关,b为负相关,c为不相关 | B. | a为负相关,b为不相关,c为正相关 | ||
| C. | a为负相关,b为正相关,c为不相关 | D. | a为正相关,b为不相关,c为负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com