
分析 可以令f(x)=x2+ax-1+2a,由题意函数的值域为R,则可得f(x)可以取所有的正数可得,△≥0,解不等式即可求解.
解答 解:∵函数y=ln(x2+ax-1+2a)的值域为R,
∴f(x)=x2+ax-1+2a可以取所有的正数可得,△≥0,
∴a2-4(2a-1)≥0,
解得a≥4+2$\sqrt{3}$或a≤4-2$\sqrt{3}$,
故答案为:(-∞,4-2$\sqrt{3}$]∪[4+2$\sqrt{3}$,+∞).
点评 本题主要考查了由二次函数与对数函数复合的复合函数,解题的关键是要熟悉对数函数的性质,解题时容易误认为△<0,要注意区别与函数的定义域为R的限制条件.


科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
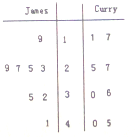 如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )
如图是NBA15-16季后赛中勒布朗-詹姆斯(LeBron James)与斯蒂芬-库里(Stephen Curry)随机抽取的8场比赛得分统计结果,则下列说法正确的是( )| A. | 他们的水平相当,但James 比Curry发挥稳定 | |
| B. | 他们的水平相当,但Curry比James 发挥稳定 | |
| C. | James比Curry水平高,也比Curry发挥稳定 | |
| D. | Curry比水平高,也比James发挥稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4<a≤0 | B. | a<-4 | C. | -4<a<0 | D. | a≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com