
【题目】已知圆![]() 上一动点
上一动点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() 点,
点,![]() 中点为
中点为![]() .
.
(1)当![]() 在圆
在圆![]() 上运动时,求点
上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,当
两点,当![]() 时,求线段
时,求线段![]() 的垂直平分线方程.
的垂直平分线方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】分析:(1)要求点![]() 的轨迹
的轨迹![]() 的方程,可设点
的方程,可设点![]() 的坐标为
的坐标为![]() ,由条件过点
,由条件过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() 点,
点,![]() 中点为
中点为![]() ,可写出点A的坐标
,可写出点A的坐标![]() 。因为点
。因为点![]() 在圆
在圆![]() 上,故可将点
上,故可将点![]() 的坐标代入圆
的坐标代入圆![]() 的方程
的方程![]() ,可得点
,可得点![]() 的轨迹
的轨迹![]() 。
。
(2)要线段![]() 的垂直平分线方程,应先求直线
的垂直平分线方程,应先求直线![]() 的方程,所以应设直线
的方程,所以应设直线![]() 的方程,根据弦长求直线
的方程,根据弦长求直线![]() 的方程。因为直线
的方程。因为直线![]() 的斜率是否存在不确定,为了避免讨论,可设直线
的斜率是否存在不确定,为了避免讨论,可设直线![]() 方程为:
方程为:![]() ,并与轨迹
,并与轨迹![]() 的方程联立可得
的方程联立可得![]() ,由根与系数的关系可得
,由根与系数的关系可得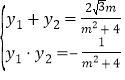 ,由弦长公式可得
,由弦长公式可得![]() ,可解得
,可解得![]() 。分情况讨论,求线段
。分情况讨论,求线段![]() 的中点,直线
的中点,直线![]() 的斜率,进而可求线段
的斜率,进而可求线段![]() 的垂直平分线方程。
的垂直平分线方程。
详解:(1)设![]() ,则
,则![]()
将![]() 代入圆
代入圆![]() 方程得:点
方程得:点![]() 的轨迹
的轨迹![]()
(注:学生不写![]() 也不扣分)
也不扣分)
(2)由题意可设直线![]() 方程为:
方程为:![]() ,
,
由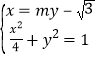 得:
得:![]()
所以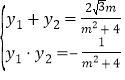
![]()
所以![]() .
.
当![]() 时,中点纵坐标
时,中点纵坐标![]() ,代入
,代入![]() 得:
得:
中点横坐标![]() ,斜率为
,斜率为![]()
故![]() 的垂直平分线方程为:
的垂直平分线方程为:![]()
当![]() 时,同理可得
时,同理可得![]() 的垂直平分线方程为:
的垂直平分线方程为:![]()
所以![]() 的垂直平分线方程为:
的垂直平分线方程为:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,设函数
,设函数![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在考察黄烟经过药物处理和发生青花病的关系时,得到如下数据:在试验的470株黄烟中,经过药物处理的黄烟有25株发生青花病,60株没有发生青花病;未经过药物处理的有185株发生青花病,200株没有发生青花病.试推断药物处理跟发生青花病是否有关系.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某技校开展技能大赛,甲、乙两班各选取5名学生加工某种零件,在4个小时内每名学生加工的合格零件数的统计数据的茎叶图如图所示,已知甲班学生在4个小时内加工的合格零件数的平均数为21,乙班学生在4个小时内加工的合格零件数的平均数不低于甲班的平均数.
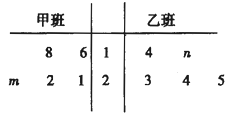
(1)求![]() 的值;
的值;
(2)分别求出甲、乙两班学生在4个小时内加工的合格零件数的方差![]() 和
和![]() ,并由此比较两班学生的加工水平的稳定性.
,并由此比较两班学生的加工水平的稳定性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com