
分析 (Ⅰ)根据奇函数的性质可知f(0)=0,求出b,a值;
(Ⅱ)利用定义的方法判断函数单调性,设?x1,x2∈(-1,1)且x1<x2,判断f(x1)-f(x2)的正负即可.
解答 解:(Ⅰ)由题知,f(x)是(-1,1)上的奇函数,
所以f(0)=0,即b=0…(3分)
又因为f($\frac{1}{2}$)=$\frac{2}{5}$.
所以a=1,
∴f(x)=$\frac{x}{1+{x}^{2}}$;
(Ⅱ)证明:?x1,x2∈(-1,1)且x1<x2,
则有f(x1)-f(x2)=$\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{(1+{{x}_{1}}^{2})(1+{{x}_{2}}^{2})}$,
∵x1<x2,x1,x2∈(-1,1),
∴f(x1)-f(x2)=$\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{(1+{{x}_{1}}^{2})(1+{{x}_{2}}^{2})}$<0,
∴f(x1)<f(x2),
∴函数在(-1,1)上是增函数.
点评 本题考查了函数的奇偶性和利用定义的方法判断函数的单调性,属于基础题型,应熟练掌握.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
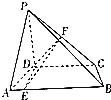 如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD.
如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 26 | ||
| 合计 | 90 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 相关人员数 | 抽取人数 | |
| 公务员 | 32 | x |
| 教师 | 48 | y |
| 自由职业者 | 64 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2016 | B. | -2015 | C. | 2016 | D. | 2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com