
���� ��1����ס��ҡ������������ѡȡ�ĺ�����ͬ�ĸ��ʣ����û����¼��ĸ��ʹ�ʽ��⼴�ɣ�
��2��Ͷ���ʽ�εĿ���ȡֵΪ300��400��500��600���ֱ�����ʣ��г��ֲ��У������������ɣ�
��� �⣺��1�������⣬P=6��$\frac{1}{6}��\frac{1}{3}��\frac{1}{2}$=$\frac{1}{6}$��
��2��Ͷ���ʽ�εĿ���ȡֵΪ300��400��500��600��
P����=300��=$\frac{1}{6}��\frac{1}{6}��\frac{1}{6}$+$\frac{1}{6}��\frac{1}{3}��\frac{1}{6}$+$\frac{1}{6}��\frac{1}{6}��\frac{1}{3}$+$\frac{1}{6}��\frac{1}{3}��\frac{1}{3}$+$\frac{1}{3}��\frac{1}{6}��\frac{1}{6}$+$\frac{1}{3}��\frac{1}{3}��\frac{1}{6}$+$\frac{1}{3}��\frac{1}{6}��\frac{1}{3}$+$\frac{1}{3}��\frac{1}{3}��\frac{1}{3}$=$\frac{1}{8}$��
P����=400��=$\frac{1}{6}��\frac{1}{6}��\frac{1}{3}$+$\frac{1}{6}��\frac{1}{2}��\frac{1}{3}$+$\frac{1}{2}��\frac{1}{6}��\frac{1}{3}$+$\frac{1}{2}��\frac{1}{2}��\frac{1}{3}$+$\frac{1}{3}��\frac{1}{6}��\frac{1}{6}$+$\frac{1}{3}��\frac{1}{6}��\frac{1}{2}$+$\frac{1}{2}��\frac{1}{3}��\frac{1}{6}$+$\frac{1}{2}��\frac{1}{3}��\frac{1}{3}$+$\frac{1}{6}��\frac{1}{2}��\frac{1}{6}$+$\frac{1}{6}��\frac{1}{2}��\frac{1}{3}$+$\frac{1}{3}��\frac{1}{2}��\frac{1}{6}$+$\frac{1}{3}��\frac{1}{2}��\frac{1}{3}$=$\frac{3}{8}$��
P����=500��=$\frac{1}{6}��\frac{1}{2}��\frac{1}{2}$+$\frac{1}{3}��\frac{1}{2}��\frac{1}{2}$+$\frac{1}{2}��\frac{1}{6}��\frac{1}{2}$+$\frac{1}{2}��\frac{1}{3}��\frac{1}{2}$+$\frac{1}{2}��\frac{1}{2}��\frac{1}{6}$+$\frac{1}{2}��\frac{1}{2}��\frac{1}{3}$=$\frac{3}{8}$��
P����=600��=$\frac{1}{2}��\frac{1}{2}��\frac{1}{2}$=$\frac{1}{8}$��
| �� | 300 | 400 | 500 | 600 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | $\frac{1}{8}$ |
���� ���⿼��ŵ���͡������¼��ĸ��ʡ���ɢ����������ķֲ��к�������֪ʶ������������ѧ֪ʶ��������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15 | B�� | -15 | C�� | 20 | D�� | -20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
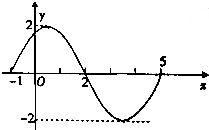 ��ͼ�Ǻ���f��x��=Asin����x+�գ���A��0���أ�0��0���գ��У���һ����ͼ��
��ͼ�Ǻ���f��x��=Asin����x+�գ���A��0���أ�0��0���գ��У���һ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ۢ� | C�� | �٢ۢ� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���߳�Ϊ2��������ABCD�У�BE=BF=$\frac{1}{4}$BC������AED����DCF�ֱ���DE��DF����ʹA��C�����غ���A��㣬������A��-EFD�����Ϊ��������
��ͼ���߳�Ϊ2��������ABCD�У�BE=BF=$\frac{1}{4}$BC������AED����DCF�ֱ���DE��DF����ʹA��C�����غ���A��㣬������A��-EFD�����Ϊ��������| A�� | $\frac{{\sqrt{21}}}{12}$ | B�� | $\frac{{\sqrt{17}}}{12}$ | C�� | $\frac{{\sqrt{21}}}{6}$ | D�� | $\frac{{\sqrt{17}}}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | $\frac{39}{5}$ | C�� | $\frac{41}{5}$ | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com