
设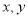 满足
满足 则
则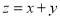 ( )
( )
A.有最小值2,最大值3 B.有最小值2,无最大值
C.有最大值3,无最小值 D.既无最小值,也无最大值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测理科数学试卷(解析版) 题型:填空题
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1, ,那么⊙O2的半径为 .
,那么⊙O2的半径为 .

查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:解答题
某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:填空题
从装有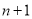 个球(其中
个球(其中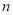 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出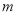 个球(
个球(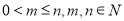 ),共有
),共有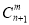 种取法.在这
种取法.在这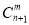 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的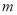 个球全部为白球,另一类是取出
个球全部为白球,另一类是取出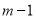 个白球,1个黑球,共有
个白球,1个黑球,共有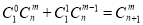 ,即有等式:
,即有等式: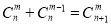 成立.试根据上述思想化简下列式子:
成立.试根据上述思想化简下列式子: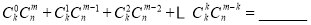 .(
.(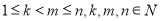 )
)
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高三上学期第二次月考理科数学试卷(解析版) 题型:解答题
如图,四边形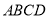 是正方形,
是正方形,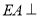 平面
平面 ,
,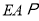
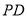 ,
,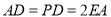 ,
,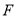 ,
,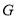 ,
, 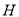 分别为
分别为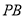 ,
,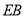 ,
,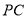 的中点.
的中点.

(1)求证: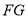
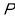 平面
平面 ;
;
(2)求平面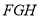 与平面
与平面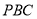 所成锐二面角的大小.
所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州市高三第二次调研考试文科数学试卷(解析版) 题型:解答题
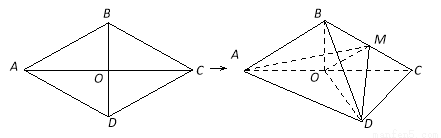
(本小题满分14分)如图,菱形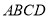 的边长为
的边长为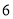 ,
,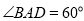 ,
,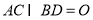 .将菱形
.将菱形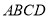 沿对角线
沿对角线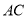 折起,得到三棱锥
折起,得到三棱锥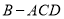 ,点
,点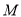 是棱
是棱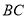 的中点,
的中点,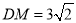 .
.
(1)求证: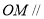 平面
平面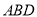 ;
;
(2)求三棱锥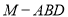 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com