
如图,四边形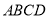 是正方形,
是正方形,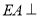 平面
平面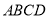 ,
,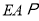
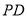 ,
,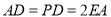 ,
,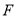 ,
,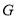 ,
, 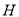 分别为
分别为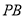 ,
,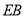 ,
,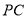 的中点.
的中点.

(1)求证: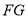
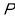 平面
平面 ;
;
(2)求平面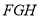 与平面
与平面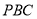 所成锐二面角的大小.
所成锐二面角的大小.
(1)证明见解析;(2)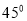
【解析】
试题分析:(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明证线线垂直,只需要证明直线的方向向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:(1)证明: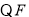 ,
,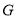 分别为
分别为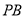 ,
,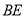 的中点,
的中点,
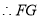
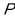
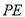 .
.
又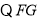
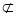 平面
平面 ,
,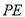
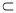 平面
平面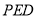 ,
,
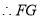
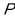 平面
平面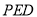 .
.
(2)解: 平面
平面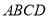 ,
,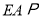
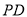 ,
, 平面
平面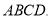
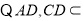 平面
平面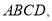
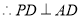 ,
,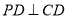 .
.
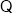 四边形
四边形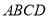 是正方形,
是正方形,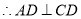 .
.
以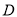 为原点,分别以直线
为原点,分别以直线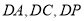 为
为 轴,
轴, 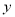 轴,
轴,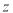 轴
轴
建立如图所示的空间直角坐标系,设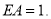
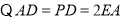 ,
,
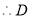
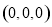 ,
,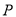
 ,
,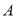
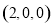 ,
,
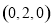 ,
,
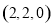 ,
, ,
,
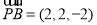 ,
,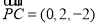 .
.
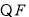 ,
,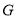 ,
, 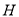 分别为
分别为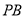 ,
,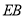 ,
,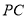 的中点,
的中点,
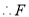
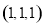 ,
,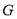
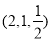 ,
,
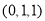 ,
,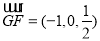 ,
,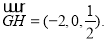

(解法一)设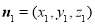 为平面
为平面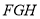 的一个法向量,则
的一个法向量,则 ,
,
即 ,令
,令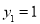 ,得
,得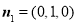 .
.
设 为平面
为平面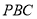 的一个法向量,则
的一个法向量,则 ,
,
即 ,令
,令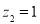 ,得
,得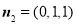 .
.
所以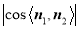 =
=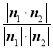 =
=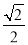 .
.
所以平面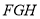 与平面
与平面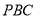 所成锐二面角的大小为
所成锐二面角的大小为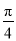 (或
(或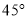 )
)
(解法二) ,
, ,
,
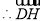 是平面
是平面 一个法向量.
一个法向量.
 ,
,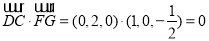 ,
,
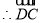 是平面平面
是平面平面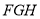 一个法向量.
一个法向量.
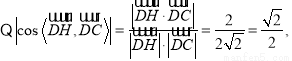
 平面
平面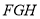 与平面
与平面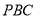 所成锐二面角的大小为
所成锐二面角的大小为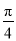 (或
(或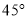 ).
).
(解法三)延长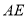 到
到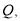 使得
使得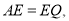 连
连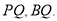

 ,
,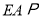
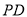 ,
,
 四边形
四边形 是平行四边形,
是平行四边形,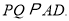
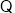 四边形
四边形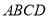 是正方形,
是正方形,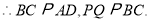
 ,
,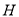 分别为
分别为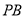 ,
,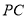 的中点,
的中点,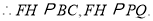
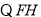
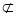 平面
平面 ,
,
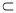 平面
平面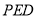 ,
, 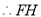
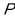 平面
平面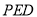 .
.
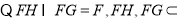 平面
平面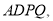
 平面
平面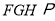 平面
平面
故平面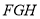 与平面
与平面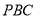 所成锐二面角与二面角
所成锐二面角与二面角 相等.
相等.
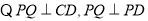
 平面
平面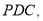
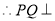 平面
平面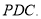
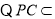 平面
平面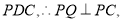
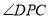 是二面角
是二面角 的平面角.
的平面角.
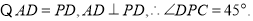
 平面
平面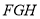 与平面
与平面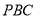 所成锐二面角的大小为
所成锐二面角的大小为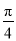 (或
(或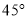 ).
).
考点:1、直线与平面平行的判定;2、平面与平面所成的角.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:选择题
设平面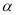 与平面
与平面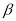 相交于直线
相交于直线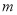 ,直线
,直线 在平面
在平面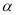 内,直线
内,直线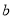 在平面
在平面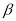 内,且
内,且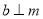 ,则“
,则“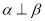 ”是“
”是“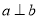 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
设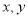 满足
满足 则
则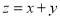 ( )
( )
A.有最小值2,最大值3 B.有最小值2,无最大值
C.有最大值3,无最小值 D.既无最小值,也无最大值.
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:选择题
用0、1、2、3、4这五个数字组成无重复数字的五位数,其中恰有一个偶数数字夹在两个奇数数字之间的五位数的个数是( )
A.48 B.36 C.28 D.12
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:选择题
对两个变量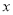 和
和 进行回归分析,得到一组样本数据:
进行回归分析,得到一组样本数据: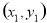 ,
,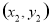 , ,
, ,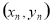 ,则下列说法中不正确的是( )
,则下列说法中不正确的是( )
A.由样本数据得到的回归方程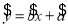 必过样本点的中心
必过样本点的中心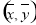
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数 来刻画回归效果,
来刻画回归效果,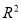 的值越小,说明模型的拟合效果越好
的值越小,说明模型的拟合效果越好
D.用相关指数 来刻画回归效果,
来刻画回归效果,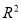 的值越 大,说明模型的拟合效果越好
的值越 大,说明模型的拟合效果越好
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高三上学期第二次月考理科数学试卷(解析版) 题型:选择题
阅读如图的程序框图,若运行相应的程序,则输出的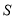 的值是( )
的值是( )

A.21 B.39 C.81 D.102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com