
【题目】已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R,对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B是有限集,则使得集合B中元素个数最少时的实数k的取值范围是__.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
其中正确结论的序号是( )
A.②④⑤B.①②④⑤C.①③④D.②③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为A(A为常数)元,之后每年会投入一笔研发资金,n年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() ,
,![]() 为常数,
为常数,![]() .已知3年后总投入资金为研发启动是投入资金的3倍,问:
.已知3年后总投入资金为研发启动是投入资金的3倍,问:
(1)研发启动多少年后,总投入资金是研发启动时投入资金的8倍;
(2)研发启动后第几年投入的资金最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P到圆(x+2)2+y2=1的切线长与到y轴的距离之比为t(t>0,t≠1);
(1)求动点P的轨迹C的方程;
(2)当![]() 时,将轨迹C的图形沿着x轴向左移动1个单位,得到曲线G,过曲线G上一点Q作两条渐近线的垂线,垂足分别是P1和P2,求
时,将轨迹C的图形沿着x轴向左移动1个单位,得到曲线G,过曲线G上一点Q作两条渐近线的垂线,垂足分别是P1和P2,求![]() 的值;
的值;
(3)设曲线C的两焦点为F1,F2,求t的取值范围,使得曲线C上不存在点Q,使∠F1QF2=θ(0<θ<π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
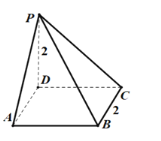
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com