
(本小题满分12分)
在平面直角坐标系中,有三个点的坐标分别是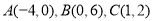 .
.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线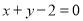 平行的直线方程;
平行的直线方程;
(3)求过C且与AB所在的直线垂直的直线方程.
(1)见解析 (2) (3)
(3)
【解析】
试题分析:注意证明平面当中的三点不共线的方法,可以应用两点所在直线的斜率不相等来处理,对应第二问需要知道两直线平行时的条件,应用点斜式方程可得结果,也可应用平行直线系方程的应用,对应第三问,要明确两直线垂直的条件,可以应用点斜式方程,也可应用垂直直线系方程,来求出对应的直线方程.
试题解析:(1)∵ , (1分)
, (1分)
 , (2分)
, (2分)
∴ , (3分)
, (3分)
∴ 三点不共线. (4分)
三点不共线. (4分)
(2)∵ 的中点坐标为
的中点坐标为 , (5分)
, (5分)
直线 的斜率
的斜率 , (6分)
, (6分)
所以满足条件的直线方程为 ,即
,即 为所求. (8分)
为所求. (8分)
(3)∵ ,∴与AB所在直线垂直的直线的斜率为
,∴与AB所在直线垂直的直线的斜率为 , (10分)
, (10分)
所以满足条件的直线方程为 ,即
,即 . (12分)
. (12分)
考点:证明三点不共线的方法,平行直线系,垂直直线系,直线方程的点斜式.


科目:高中数学 来源:2014-2015学年内蒙古赤峰市宁城县高二上学期期末考试理科数学试卷(解析版) 题型:选择题
若不等式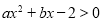 的解集为
的解集为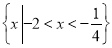 ,则
,则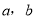 的值分别是( )
的值分别是( )
(A)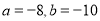 (B)
(B)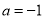 ,
,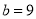 (C)
(C)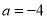 ,
,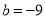 (D)
(D) ,
,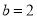
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知椭圆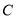 的两个焦点的坐标分别为
的两个焦点的坐标分别为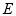
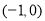 ,
,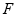
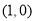 ,并且经过点(
,并且经过点(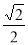 ,
,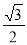 ),M、N为椭圆
),M、N为椭圆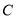 上关于
上关于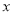 轴对称的不同两点.
轴对称的不同两点.
(1)求椭圆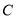 的标准方程;
的标准方程;
(2)若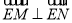 ,试求点
,试求点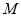 的坐标;
的坐标;
(3)若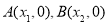 为
为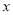 轴上两点,且
轴上两点,且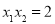 ,试判断直线
,试判断直线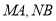 的交点
的交点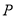 是否在椭圆
是否在椭圆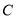 上,并证明你的结论.
上,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市高二上学期期末考试文科数学试卷(解析版) 题型:选择题
直线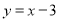 与抛物线
与抛物线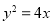 交于A、B两点,过A、B两点向抛物线的准线
交于A、B两点,过A、B两点向抛物线的准线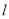 作垂线,垂足分别为P、Q,则梯形APQB的面积为
作垂线,垂足分别为P、Q,则梯形APQB的面积为
A.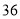 B.
B.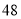 C.
C.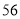 D.
D.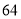
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知直线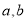 与平面
与平面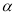 ,则下列四个命题中假命题是
,则下列四个命题中假命题是
A.如果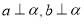 ,那么
,那么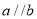 B.如果
B.如果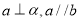 ,那么
,那么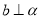
C.如果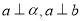 ,那么
,那么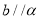 D.如果
D.如果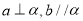 ,那么
,那么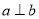
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com