
【题目】甲题型:给出如图数阵表格形式,表格内是按某种规律排列成的有限个正整数.
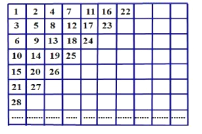
(1)记第一行的自左至右构成数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,试求;
项和,试求;
(2)记![]() 为第
为第![]() 列第
列第![]() 行交点的数字,观察数阵请写出
行交点的数字,观察数阵请写出![]() 表达式,若
表达式,若![]() ,试求出
,试求出![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数fn(x)=xn+bx+c(n∈Z,b,c∈R).
(1)若n=﹣1,且f﹣1(1)=f﹣1(![]() )=5,试求实数b,c的值;
)=5,试求实数b,c的值;
(2)设n=2,若对任意x1,x2∈[﹣1,1]有|f2(x1)﹣f2(x2)|≤6恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的对称轴与准线的交点,点
的对称轴与准线的交点,点![]() 为抛物线的焦点,
为抛物线的焦点,![]() 在抛物线上且满足
在抛物线上且满足![]() ,当
,当![]() 取最大值时,点
取最大值时,点![]() 恰好在以
恰好在以![]() ,
,![]() 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情爆发以来,疫情防控牵挂着所有人的心. 某市积极响应上级部门的号召,通过沿街电子屏、微信公众号等各种渠道对此战“疫”进行了持续、深入的悬窗,帮助全体市民深入了解新冠状病毒,增强战胜疫情的信心. 为了检验大家对新冠状病毒及防控知识的了解程度,该市推出了相关的知识问卷,随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
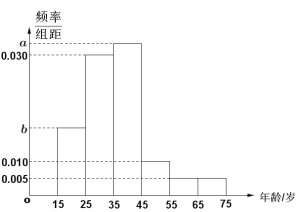
(1)求图中![]() 的值;
的值;
(2)现采取分层抽样在![]() 和
和![]() 中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的2×2列联表,并根据统计结果判断:能够有99.9%的把握认为“中老年人”比“青少年人”更加了解防控的相关知识?
了解全面 | 了解不全面 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
附表及公式: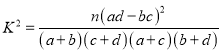 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,
,![]() 其图象上任意一点
其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,抛物线
,抛物线![]() 的焦点与点
的焦点与点![]() 重合,点
重合,点![]() 是抛物线与双曲线的一个交点,如图所示.
是抛物线与双曲线的一个交点,如图所示.
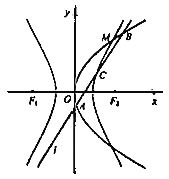
(1)求双曲线及抛物线的标准方程;
(2)设直线![]() 与双曲线的过一、三象限的渐近线平行,且交抛物线于
与双曲线的过一、三象限的渐近线平行,且交抛物线于![]() 两点,交双曲线于点
两点,交双曲线于点![]() ,若点
,若点![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2
(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com