
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |

分析 (1)由已知条件能求出图中各组的纵坐标,由此能完成被调查人员的频率分布直方图.
(2)ξ的所有可能取值为:0,1,2,3,分别求出p(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出随机变量ξ的分布列和数学期望.
解答 解:(1)各年龄段的频率分别是0.1,0.2,0.3,0.2,0.1,0.1,
∴图中各年龄段的纵坐标分别是0.01,0.02,0.03,0.02,0.01,0.01.
∴被调查者的频率分布直方图如图所示: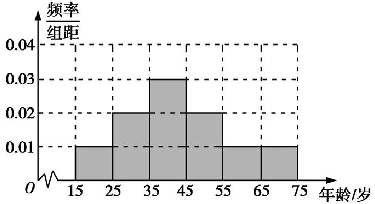
(2)ξ 的所有可能取值为0,1,2,3,
P(ξ=0)=$\frac{{C}_{4}^{2}•{C}_{6}^{2}}{{C}_{5}^{2}•{C}_{10}^{2}}$=$\frac{15}{75}$=$\frac{1}{5}$,
P(ξ=1)═$\frac{{C}_{4}^{1}•{C}_{6}^{2}}{{{C}_{5}^{2}C}_{10}^{2}}$+$\frac{{C}_{4}^{2}•{C}_{4}^{1}•{C}_{6}^{1}}{{C}_{5}^{2}•{C}_{10}^{2}}$=$\frac{34}{75}$,
P(ξ=2)=$\frac{{C}_{4}^{1}•{C}_{4}^{1}•{C}_{6}^{1}}{{C}_{5}^{2}•{C}_{10}^{2}}$+$\frac{{C}_{4}^{2}•{C}_{4}^{2}}{{C}_{5}^{2}•{C}_{10}^{2}}$=$\frac{22}{75}$,
P(ξ=3)=$\frac{{C}_{4}^{1}•{C}_{4}^{2}}{{C}_{5}^{2}•{C}_{10}^{2}}$=$\frac{4}{75}$,…(7分)
所以ξ的分布列是:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{34}{75}$ | $\frac{22}{75}$ | $\frac{4}{75}$ |
点评 本题考查频率直方图的作法,考查随机变量ξ的分布列和数学期望,解题时要认真审题,注意排列组合思想的合理运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (4,3) | B. | {4,-3} | C. | {(4,3)} | D. | {(4,-3)} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{1}{16}$ | B. | x=-$\frac{1}{16}$ | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | (1,$\frac{3}{2}$] | C. | [0,$\frac{3}{2}$] | D. | (0,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第二象限角比第一象限角大 | |
| B. | 60°角与600°角是终边相同角 | |
| C. | 三角形的内角是第一象限角或第二象限角 | |
| D. | 将表的分针拨慢10分钟,则分针转过的角的弧度数为$\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com