
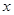 的方程
的方程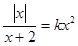 有四个不同的实数解,则实数
有四个不同的实数解,则实数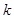 的取值范围为()
的取值范围为() A. | B. | C. | D. |

 ,方程化为
,方程化为 ,
, 满足上述方程,是方程的一个根
满足上述方程,是方程的一个根
 有
有
 则方程变为
则方程变为 ,即
,即
 则方程变为
则方程变为 即
即
 ,(1)(2)均无解。显然
,(1)(2)均无解。显然 不是(1)(2)的解
不是(1)(2)的解 是原方程的根,则要求方程(1)(2)有3个根
是原方程的根,则要求方程(1)(2)有3个根 ,则
,则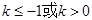 .
. ,解得
,解得 ,
,
 ,则(1)有两个不相等实根,两根之积为
,则(1)有两个不相等实根,两根之积为 ,两根之和为
,两根之和为 ,说明两根均为负值,但(1)方程前提条件是
,说明两根均为负值,但(1)方程前提条件是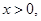 ,因此
,因此 时方程(1)在
时方程(1)在 前提下无解,原方程不可能有4个不同的实数根。
前提下无解,原方程不可能有4个不同的实数根。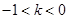 ,(1)方程无根,原方程不可能有4个不同的实数根。
,(1)方程无根,原方程不可能有4个不同的实数根。 ,(2)方程无根,原方程不可能有4个不同的实数根。
,(2)方程无根,原方程不可能有4个不同的实数根。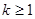 ,方程(1)有两个不相等实根,两根之积为
,方程(1)有两个不相等实根,两根之积为 ,两根之和为
,两根之和为 ,说明有一个正根一个负根,在
,说明有一个正根一个负根,在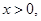 前提下,只有一个正根,则要求(2)有两个不相等的负根。则
前提下,只有一个正根,则要求(2)有两个不相等的负根。则 .要求
.要求 .
. ,两根之和为
,两根之和为 , 两根之积
, 两根之积 ,说明(2)有两个不相等的负根,之前要求
,说明(2)有两个不相等的负根,之前要求 ,对(2),若
,对(2),若 ,则
,则 ,显然
,显然 不是方程的根。
不是方程的根。 .
.

 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:不详 题型:解答题
| a |
| 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
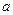 克,现在向糖水中再加
克,现在向糖水中再加 克糖,此时糖水变得更甜了.(其中
克糖,此时糖水变得更甜了.(其中 ).
).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com