Question

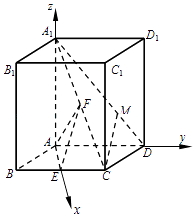
【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面四边形ABCD为菱形，A1A=AB=2，∠ABC= ，E，F分别是BC，A1C的中点．
（1）求异面直线EF，AD所成角的余弦值；
（2）点M在线段A1D上， =λ．若CM∥平面AEF，求实数λ的值．

Answer 1

【答案】
（1）解：因为四棱柱ABCD﹣A1B1C1D1为直四棱柱，

所以A1A⊥平面ABCD．

又AE平面ABCD，AD平面ABCD，

所以A1A⊥AE，A1A⊥AD．

在菱形ABCD中∠ABC= ，则△ABC是等边三角形．

因为E是BC中点，所以BC⊥AE．

因为BC∥AD，所以AE⊥AD．

建立空间直角坐标系．则A（0，0，0），C（ ，1，0），D（0，2，0），

A1（0，0，2），E（ ，0，0），F（ ， ，1）．

=（0，2，0）， =（﹣ ， ，1），

所以异面直线EF，AD所成角的余弦值为 =

（2）解：设M（x，y，z），由于点M在线段A1D上，且 =λ，

则（x，y，z﹣2）=λ（0，2，﹣2）．

则M（0，2λ，2﹣2λ）， =（﹣ ，2λ﹣1，2﹣2λ）．

设平面AEF的法向量为 =（x0，y0，z0）．

因为 =（ ，0，0）， =（ ， ，1），

由 ，得x0=0， y0+z0=0．

取y0=2，则z0=﹣1，

则平面AEF的一个法向量为n=（0，2，﹣1）

由于CM∥平面AEF，则 =0，即2（2λ﹣1）﹣（2﹣2λ）=0，解得λ= ．

【解析】（1）建立坐标系，求出直线的向量坐标，利用夹角公式求异面直线EF，AD所成角的余弦值；（2）点M在线段A1D上， =λ．求出平面AEF的法向量，利用CM∥平面AEF，即可求实数λ的值．
【考点精析】掌握异面直线及其所成的角和直线与平面平行的性质是解答本题的根本，需要知道异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行．