
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,±3) | B. | (±3,0) | C. | (±1,0) | D. | (0,±1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
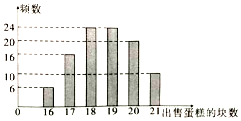 某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图:
某蛋糕店出售一种蛋糕,这种蛋糕的保质期很短,必须当天卖掉,否则容易变质,该蛋糕店每天以每块16元的成本价格制作这种蛋糕若干块,然后以每块26元的价格出售,如果当天卖不完,剩下的蛋糕只能以每块6元低价出售.蛋糕店记录了100天该种蛋糕的日需求量n(单位:块,n∈N*)整理得如图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com