
已知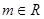 ,对
,对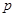 :
: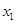 和
和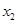 是方程
是方程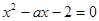 的两个根,不等式
的两个根,不等式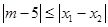 对任意实数
对任意实数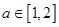 恒成立;
恒成立;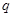 :函数
:函数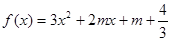 有两个零点,求使“
有两个零点,求使“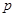 且
且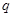 ”为真命题的实数的取值范围。
”为真命题的实数的取值范围。
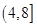
解析试题分析:利用二次方程的韦达定理求出|x1-x2|,将不等式恒成立转化为求函数的最值,求出命题p为真命题时m的范围;利用二次方程有两个不等根判别式大于0,求出命题Q为真命题时m的范围;P且Q为真转化为两个命题全真,求出m的范围.解:由题设x1+x2=a,x1x2=-2,∴|x1-x2|=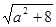 .当a∈[1,2]时,
.当a∈[1,2]时,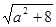 的最小值为3.要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+
的最小值为3.要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+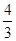 =0的判别式△=4m2-12(m+
=0的判别式△=4m2-12(m+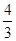 )=4m2-12m-16>0,得m<-1或m>4.综上,要使“p且q”为真命题,只需P真Q真,即2≤m≤8,m<-1或m>4,解得实数m的取值范围是(4,8].
)=4m2-12m-16>0,得m<-1或m>4.综上,要使“p且q”为真命题,只需P真Q真,即2≤m≤8,m<-1或m>4,解得实数m的取值范围是(4,8].
考点:二次方程的韦达定理
点评:本题考查二次方程的韦达定理、二次方程有根的判断、复合命题的真假与构成其简单命题的真假的关系.


科目:高中数学 来源: 题型:解答题
设p:实数x满足x2-4ax+3a2<0(其中a≠0),q:实数x满足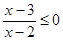
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com