
【题目】如图1:已知正方形ABCD的边长是2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A.设点M经过的路程为x,△ABM的面积为S. 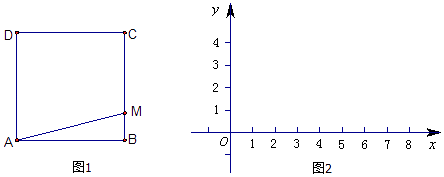
(1)求函数S=f(x)的解析式及其定义域;
(2)在图2中画出函数S=f(x)的图象.
【答案】
(1)解:由题意,当M从B到C时, ![]() =x,(0≤x≤2)
=x,(0≤x≤2)
当M从C到D时,S△ABM= ![]() ABBC=2(2<x≤4),
ABBC=2(2<x≤4),
当M从D到A时,S△ABM= ![]() AB(6﹣x)=6﹣x(4<x≤6),
AB(6﹣x)=6﹣x(4<x≤6),
函数S=f(x)= 
其定义域为{x|0≤x≤6}
(2)解:由(1)的解析式可得:当0≤x≤2时,f(x)=x,值域为[0,2],
当2<x≤4时,f(x)=2,值域为{2}
当4<x≤6时,f(x)=6﹣x,值域为[0,2).
故图象如下:

【解析】(1)由题意,当M从B到C过程,三角形ABM的面积为S随x的增大而增大,当M从C到D过程,三角形ABM的面积为S随x的增大而不变,当M从D到A过程,三角形ABM的面积为S随x的增大而减小.分段函数,可得解析式及其定义域.(2)根据(1)的函数关系式,求值域,作图即可.


科目:高中数学 来源: 题型:
【题目】加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”,在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据,根据上述函数模型和实验数据,可以得到最佳加工时间为( ) 
A.3.50分钟
B.3.75分钟
C.4.00分钟
D.4.25分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若变量x,y满足约束条件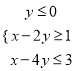 ,则z=3x+5y的取值范围是( )
,则z=3x+5y的取值范围是( )
A. [3,+∞) B. [﹣8,3] C. (﹣∞,9] D. [﹣8,9]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( ) 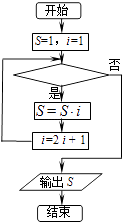
A.i≤31?
B.i≤63?
C.i≥63?
D.i≤127?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.
B.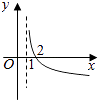
C.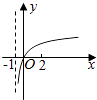
D.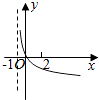
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
)x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
(1)求集合A∩B,(UB)∪A;
(2)若A∪C=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为右焦点,直线
为右焦点,直线![]() 与
与![]() 的交点到
的交点到![]() 轴的距离为
轴的距离为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
, ![]() 为
为![]() 上异于点
上异于点![]() 的一点,以
的一点,以![]() 为直径作圆
为直径作圆![]() .
.
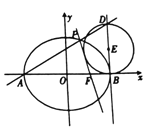
(1)求![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,证明:直线
,证明:直线![]() 与圆
与圆![]() 相切.
相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com