练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的离心率为，椭圆与轴交于 两点，且．

    （1）求椭圆的方程；

    （2）设点是椭圆上的一个动点，且直线与直线分别交于 两点．是否存在点使得以 为直径的圆经过点？若存在，求出点的横坐标；若不存在，说明理由.

    【答案】（1）；（2）点不存在.

    【解析】分析：（1）根据椭圆的几何性质知，即，再由离心率得，从而可得，得椭圆方程；

    （2）假设点P存在，并设，写出PA的方程，求出M点坐标，同理得N点坐标，求出MN的中点坐标，即圆心坐标，利用圆过点D得一关于的等式，把P点坐标代入椭圆方程后也刚才的等式联立解得，注意的范围，即可知存在不存在．

    详解：（1）由已知，得知，

    又因为离心率为，所以.

    因为，所以,

    所以椭圆的标准方程为.

    （2）假设存在.

    设

    由已知可得，

    所以的直线方程为，

    的直线方程为，

    令，分别可得，，

    所以，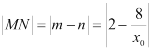

    线段的中点，

    若以为直径的圆经过点D（2,0），

    则,

    因为点在椭圆上，所以，代入化简得，

    所以， 而，矛盾，

    所以这样的点不存在.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】双曲线 的左、右焦点分别为，过作倾斜角为的直线与轴和双曲线的右支分别交于两点，若点平分线段，则该双曲线的离心率是（ ）

    A. B. C. 2 D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个工厂在某年连续10个月每月产品的总成本y（万元）与该月产量x（万件）之间有如下一组数据：

    x

    1.08

    1.12

    1.19

    1.28

    1.36

    1.48

    1.59

    1.68

    1.80

    1.87

    y

    2.25

    2.37

    2.40

    2.55

    2.64

    2.75

    2.92

    3.03

    3.14

    3.26

    （1）通过画散点图，发现可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

    （2）①建立月总成本y与月产量x之间的回归方程；

    ②通过建立的y关于x的回归方程，估计某月产量为1.98万件时，此时产品的总成本为多少万元？

    （均精确到0.001）

    附注：①参考数据：，

    ，

    ②参考公式：相关系数，

    回归方程中斜率和截距的最小二乘估计公式分别为：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】武汉市摄影协会准备在2020年1月举办主题为“我们都是追梦人”摄影图片展，通过平常人的镜头记录国强民富的幸福生活，摄影协会收到了来自社会各界的大量作品，打算从众多照片中选取100张照片展出，其参赛者年龄集中在之间，根据统计结果，做出频率分布直方图如图：

    （1）求频率直方图中的值，并根据频率直方图，求这100位摄影者年龄的中位数；

    （2）为了展示不同年龄作者眼中的幸福生活，摄影协会按照分层抽样的方法，计划从这100件照片中抽出20个最佳作品，并邀请相应作者参加“讲述照片背后的故事”座谈会．

    ①在答题卡上的统计表中填出每组相应抽取的人数：

    年龄

    人数

    ②若从年龄在的作者中选出2人把这些图片和故事整理成册，求这2人中至少有1人的年龄在的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果，各产地的包装规格相同,它们的批发价格（元/箱）和市场份额如下：

    产地

    批发价格

    市场份额

    市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.

    （1）从该地批发市场销售的富士苹果中随机抽取一箱，求该箱苹果价格低于元的概率；

    （2）按市场份额进行分层抽样，随机抽取箱富士苹果进行检验，

    ①从产地共抽取箱,求的值；

    ②从这箱苹果中随机抽取两箱进行等级检验，求两箱产地不同的概率；

    （3）由于受种植规模和苹果品质的影响，预计明年产地的市场份额将增加，产地的市场份额将减少，其它产地的市场份额不变，苹果销售价格也不变（不考虑其它因素）.设今年苹果的平均批发价为每箱元，明年苹果的平均批发价为每箱元，比较的大小.（只需写出结论）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足：a1+a2+a3+…+an=n-an，（n=1，2，3，…）

    （Ⅰ）求证：数列{an-1}是等比数列；

    （Ⅱ）令bn=（2-n）（an-1）（n=1，2，3，…），如果对任意n∈N*，都有bn+t≤t2，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (I)求曲线在点处的切线方程；

    (Ⅱ)当时，求证：函数存在极小值；

    (Ⅲ)请直接写出函数的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】每年圣诞节，各地的餐馆都出现了用餐需预定的现象，致使--些人在没有预定的情况下难以找到用餐的餐馆，针对这种现象，专家对人们“用餐地点"以及“性别”作出调查，得到的情况如下表所示:

    在家用餐

    在餐馆用餐

    总计

    女性

    男性

    总计

    (1)完成上述列联表；

    (2)根据表中的数据，试通过计算判断是否有的把握说明“用餐地点”与“性别"有关；

    (3)若在接受调查的所有人男性中按照“用餐地点”进行分层抽样，随机抽取人，再在人中抽取人赠送餐馆用餐券，记收到餐馆用餐券的男性中在餐馆用餐的人数为，求的分布列和数学期望.

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示,直角梯形中,,,,四边形为矩形,.

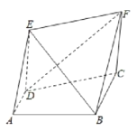
    （1）求证:平面平面;

    （2）在线段上是否存在点,使得直线与平面所成角的正弦值为,若存在,求出线段的长,若不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案