练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知矩阵A=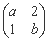有一个属于特征值1的特征向量.

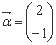      (Ⅰ) 求矩阵A；

      (Ⅱ) 若矩阵B=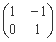，求直线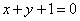先在矩阵A，再在矩阵B的对应变换作用下的像的方程. 


    【解析】(Ⅰ)由已知得，所以 …………2分

        解得  故A=.   ……………………………………………………3分

     (Ⅱ)  BA==，因为矩阵BA 所对应的线性变换将直线变成直线（或点），所以可取直线上的两点（0，1），（-1，2），……………………………4分

    ，，由得：（0，1），（-1，2）在矩阵A所对应的线性变换下的像是点（1，-3），（-1，-1）  ……………………………6分

    从而直线在矩阵BA所对应的线性变换下的像的方程为.…………7分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在中，.如果一个椭圆通过、两点，它的一个焦点为点，另一个焦点在边上，则这个椭圆的焦距为           ．  

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若两个平面的法向量分别是，则这两个平面所成的锐二面角的度数是          。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，则二项式展开式中的项的系数为（    ） 

     A .           B.  20        C.      D.  160

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某超市在节日期间进行有奖促销，凡在该超市购物满300元的顾客，将获得一次摸奖机会，规则如下：

    奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就要将奖盒中的球全部摸出才停止．规定摸到红球奖励10元，摸到白球或黄球奖励5元，摸到黑球不奖励．

    （Ⅰ）求1名顾客摸球3次停止摸奖的概率；

    （Ⅱ）记为1名顾客摸奖获得的奖金数额，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合，，若任取，则的概率为                 

    A．              B．                C．                D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数是奇函数且,当时, (),则

       实数的值为

       A．             B．              C．                 D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列，则“”是“为递增数列” 的

    （A）充分不必要条件               （B）必要不充分条件

    （C）充要条件                     （D）既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数，

    （1）若不等式的解集．求的值；

    （2）若求的最小值．

    查看答案和解析>>

    同步练习册答案