
已知函数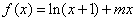 ,当
,当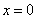 时,函数
时,函数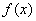 取得极大值.
取得极大值.
(1)求实数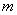 的值;
的值;
(2)已知结论:若函数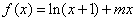 在区间
在区间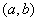 内导数都存在,且
内导数都存在,且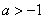 ,则存在
,则存在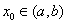 ,使得
,使得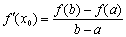 .试用这个结论证明:若
.试用这个结论证明:若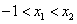 ,函数
,函数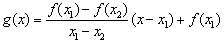 ,则对任意
,则对任意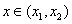 ,都有
,都有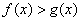 ;
;
(3)已知正数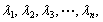 满足
满足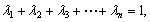 求证:当
求证:当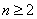 ,
,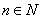 时,对任意大于
时,对任意大于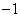 ,且互不相等的实数
,且互不相等的实数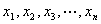 ,都有
,都有
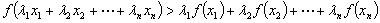
科目:高中数学 来源: 题型:
给出下列结论:
(1)在回归分析中,可用相关指数R2的值判断模型的拟合效果,R2越大,
模型的拟合效果越好;
(2)某工产加工的某种钢管,内径与规定的内径尺寸之差是离散型随机变量;
(3)随机变量的方差和标准差都反映了随机变量的取值偏离于均值的平均程度,
它们越小,则随机变量偏离于均值的平均程度越小;
(4)若关于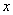 的不等式
的不等式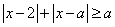 在
在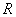 上恒成立,则
上恒成立,则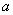 的最大值是1;
的最大值是1;
(5)甲、乙两人向同一目标同时射击一次,事件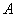 :“甲、乙中至少一人击中目标”与事件
:“甲、乙中至少一人击中目标”与事件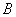 :“甲,乙都没有击中目标”是相互独立事件。
:“甲,乙都没有击中目标”是相互独立事件。
其中结论正确的是 。(把所有正确结论的序号填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
在下面的四个图象中,其中一个图象是函f(x)=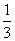 x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)等于( ).
A.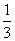 B.-
B.-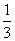 C.
C.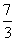 D.-
D.-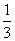 或
或 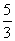
查看答案和解析>>
科目:高中数学 来源: 题型:
三棱锥P-ABC的高PO=8,AC=BC=3,∠ACB=30°,M、N 分别在BC和PO上,且CM=x,PN=2CM,则下面四个图象中大致描绘了三棱锥N-AMC的体积V与x变化关系(x∈(0,3))是 ( )
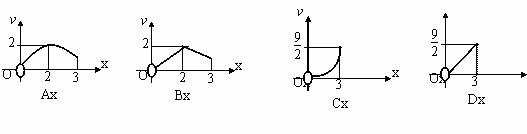
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com