【题目】已知数列{an}满足
，且
．
(1)求证：数列
是等差数列，并求出数列
的通项公式；
(2)求数列的前
项和
.
【答案】(1) an＝(2n－1)2n－1;(2) Sn＝(2n－3)2n＋3.
【解析】
（1）根据等差数列的定义，判断数列
是等差数列，并写出它的通项公式以及{an}的通项公式；
（2）根据数列{an}的前n项和定义，利用错位相减法求出Sn；
(1)证明：因为an＝2an－1＋2n，所以
＝
＝
＋1，
即－＝1，所以数列
是等差数列，且公差d＝1，其首项
＝
，所以＝＋(n－1)×1＝n－，解得an＝
×2n＝(2n－1)2n－1.
(2)Sn＝1×20＋3×21＋5×22＋…＋(2n－1)×2n－1，①
2Sn＝1×21＋3×22＋5×23＋…＋(2n－3)×2n－1＋(2n－1)×2n，②
①－②，得－Sn＝1×20＋2×21＋2×22＋…＋2×2n－1－(2n－1)2n
＝1＋
－(2n－1)2n＝(3－2n)2n－3.
所以Sn＝(2n－3)2n＋3.
期末宝典单元检测分类复习卷系列答案科目：高中数学 来源： 题型：
【题目】有下列四个命题：
①若p是q的充分不必要条件，则￢p是￢q的必要不充分条件；
②若命题p：x≥0，x2+1＞0，则￢p：x0＜0，x02+1≤0；
③在△ABC中，A＞B是sinA＞sinB的充要条件；
④命题：当1＜t＜4时方程
1表示焦点在x轴上的椭圆，为真命题．
其中真命题的序号是_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两台机床生产同一型号零件，记生产的零件的尺寸为
，相关行业质检部门规定：若
，则该零件为优等品；若
，则该零件为中等品；其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件，经质里检测得到下表数据：
尺寸 |
|
|
|
|
|
|
甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
（Ⅰ）设生产每件产品的利润为：优等品3元，中等品1元，次品亏本1元.若将频率视为概率，试估算甲机床生产一件零件的利润的数学期望；
（Ⅱ）根据已知条件完成下面的列联表，并据此数据回答：是否有
的把握认为“零件优等与否和所用机床有关”？
甲机床 | 乙机床 | 合计 | |
优等品 | |||
非优等品 | |||
合计 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图l，在边长为2的菱形
中，
，
于点
，将
沿
折起到
的位置，使
，如图2.
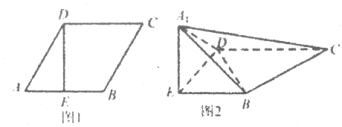
（1）求证：
平面
；
（2）求二面角
的余弦值；
（3）在线段
上是否存在点
，使平面
平面
？若存在，求
的值；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
经过点
离心率
.
（Ⅰ）求椭圆的方程；
（Ⅱ）经过椭圆左焦点
的直线(不经过点
且不与
轴重合)与椭圆交于
两点，与直线
:
交于点
，记直线
的斜率分别为
.则是否存在常数
，使得向量
共线？若存在求出的值；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为弘扬民族古典文化，市电视台举行古诗词知识竞赛，某轮比赛由节目主持人随机从题库中抽取题目让选手抢答，回答正确将给该选手记正10分，否则记负10分．根据以往统计，某参赛选手能答对每一个问题的概率均为
；现记“该选手在回答完
个问题后的总得分为
”．
（1）求
且
（
）的概率；
（2）记
，求
的分布列，并计算数学期望
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
