
甲、乙等五名奥运志愿者被随机地分到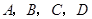 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加
四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量
岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,
岗位服务的人数,  可取何值?请求出相应的
可取何值?请求出相应的 值的分布列.
值的分布列.
科目:高中数学 来源: 题型:解答题
一个盒子装有6张卡片,上面分别写着如下6个定义域为R的函数: ,
, ,
, ,
, ,
, ,
, .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2011年4月28日世界园艺博览会将在陕西西安浐灞生态区举行,为了接待来自国内外的各界人士,需招募一批志愿者,要求志愿者不仅要有一定的气质,还需有丰富的人文、地理、历史等文化知识。志愿者的选拔分面试和知识问答两场,先是面试,面试通过后每人积60分,然后进入知识问答。知识问答有A,B,C,D四个题目,答题者必须按A,B,C,D顺序依次进行,答对A,B,C,D四题分别得20分、20分、40分、60分,每答错一道题扣20分,总得分在面试60分的基础上加或减。答题时每人总分达到100分或100分以上,直接录用不再继续答题;当四道题答完总分不足100分时不予录用。
假设志愿者甲面试已通过且第二轮对A,B,C,D四个题回答正确的概率依次是 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ) 用X表示志愿者甲在知识问答结束时答题的个数,求X的分布列和数学期望;
(Ⅱ)求志愿者甲能被录用的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某班从6名班干部中(男生4人,女生2人)选3人参加学校义务劳动;(1)求男生甲或女生乙被选中的概率;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率;
(3)设所选3人中女生人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某市文化馆在春节期间举行高中生“蓝天海洋杯”象棋比赛,规则如下:两名选手比赛时,每局胜者得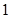 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响.
(Ⅰ)求比赛进行 局结束,且乙比甲多得
局结束,且乙比甲多得 分的概率;
分的概率;
(Ⅱ)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
根据公安部最新修订的《机动车驾驶证申领和使用规定》:每位驾驶证申领者必须通过《科目一》(理论科目)、《综合科》(驾驶技能加科目一的部分理论)的考试.已知李先生已通过《科目一》的考试,且《科目一》的成绩不受《综合科》的影响,《综合科》三年内有5次预约考试的机会,一旦某次考试通过,便可领取驾驶证,不再参加以后的考试,否则就一直考到第5次为止.设李先生《综合科》每次参加考试通过的概率依次为0.5,0.6,0.7,0.8,0.9.
(1)求在三年内李先生参加驾驶证考试次数 的分布列和数学期望;
的分布列和数学期望;
(2)求李先生在三年内领到驾驶证的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知函数 (
(
 )
)
(1)若 从集合
从集合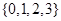 中任取一个元素,
中任取一个元素, 从集合
从集合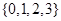 中任取一个元素,求方程
中任取一个元素,求方程 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 从区间
从区间 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数,求方程
中任取一个数,求方程 没有实根的概率.
没有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)一个口袋内装有大小相同的6个小球,其中2个红球,记为A1、A2,4个黑球,记为B1、B2、B3、B4,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出的两个球颜色不同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com