
某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数的数学期望.
科目:高中数学 来源: 题型:解答题
袋中有大小相同的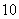 个编号为
个编号为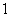 、
、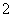 、
、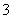 的球,
的球,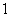 号球有
号球有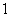 个,
个,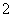 号球有
号球有 个,
个,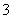 号球有
号球有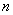 个.从袋中依次摸出
个.从袋中依次摸出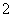 个球,已知在第一次摸出
个球,已知在第一次摸出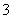 号球的前提下,再摸出一个
号球的前提下,再摸出一个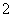 号球的概率是
号球的概率是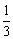 .
.
(Ⅰ)求 、
、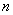 的值;
的值;
(Ⅱ)从袋中任意摸出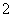 个球,记得到小球的编号数之和为
个球,记得到小球的编号数之和为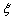 ,求随机变量
,求随机变量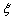 的分布列和数学期望
的分布列和数学期望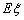 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
两个人射击,甲射击一次中靶概率是 ,乙射击一次中靶概率是
,乙射击一次中靶概率是 ,
,
(Ⅰ)两人各射击1次,两人总共中靶至少1次就算完成目标,则完成目标概率是多少?
(Ⅱ)两人各射击2次,两人总共中靶至少3次就算完成目标,则完成目标的概率是多少?
(Ⅲ)两人各射击5次,两人总共中靶至少1次的概率是否超过99%?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校在开展学雷锋活动中,从高二甲乙两班各选3名学生参加书画比赛,其中高二甲班选出了1女2男,高二乙班选出了1男2女。
(1)若从6个同学中抽出2人作活动发言,写出所有可能的结果,并求高二甲班女同学,高二乙班男同学至少有一个被选中的概率。
(2)若从高二甲班和高二乙班各选一名现场作画,写出所有可能的结果,并求选出的2名同学性别相同的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)甲盒中有红,黑,白三种颜色的球各3个,乙盒子中有黄,黑,白三种颜色的球各2个,从两个盒子中各取1个球,求取出的两个球是不同颜色的概率。
(2)在单位圆的圆周上随机取三点A、B、C,求 是锐角三角形的概率。
是锐角三角形的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙等五名奥运志愿者被随机地分到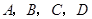 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加
四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量
岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,
岗位服务的人数,  可取何值?请求出相应的
可取何值?请求出相应的 值的分布列.
值的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设关于 的一元二次方程
的一元二次方程 .
.
(1)若 ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率;
(2)若 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字, 是从区间[1,4]中任取的数字,求方程有实根的概率.
是从区间[1,4]中任取的数字,求方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com