若以连续掷两次骰子分别得到的点数m、n作为点P的坐标
，求：
（1）点P在直线
上的概率；
（2）点P在圆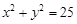
外的概率。
(1) 
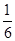；(2)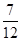 
。
解析试题分析：（1）
科目：高中数学
来源：
题型：解答题
“H7N9禽流感”问题越来越引起社会关注，我校对高一600名学生进行了一次“H7N9禽流感”知识测试，并从中抽取了部分学生的成绩（满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．
科目：高中数学
来源：
题型：解答题
某广场上有4盏装饰灯，晚上每盏灯都随机地闪烁红灯或绿灯，每盏灯出现红灯的概率都是
科目：高中数学
来源：
题型：解答题
在平面
科目：高中数学
来源：
题型：解答题
为了防止受到核污染的产品影响我国民众的身体健康，要求产品进入市场前必须进行两轮核放射检测，只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为
科目：高中数学
来源：
题型：解答题
某中学校本课程共开设了A，B，C，D共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：
科目：高中数学
来源：
题型：解答题
（本小题满分12分）某班从6名班干部中（男生4人，女生2人）选3人参加学校义务劳动；（1）求男生甲或女生乙被选中的概率；
科目：高中数学
来源：
题型：解答题
（本小题满分12分）盒子里装有6件包装完全相同的产品，已知其中有2件次品，其余4件是合格品。为了找到2件次品，只好将盒子里的这些产品包装随机打开检查，直到两件次品被全部检查或推断出来为止。记
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 
练习册系列答案
每课一练（福建）系列答案
智能达标AB卷系列答案
智慧金卷26套系列答案
单元加期末冲刺100分系列答案
高效课堂互动英语系列答案
初中全程导学导练系列答案
期末总复习系列答案
B卷周计划系列答案
天利38套初中名校期末联考测试卷系列答案
相关习题
（1）填写答题卡频率分布表中的空格，补全频率分布直方图,并标出每个小矩形对应的纵轴数据；
（2）试估计该年段成绩在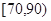
段的有多少人；
（3）请你估算该年级的平均分.
，出现绿灯的概率都是
．记这4盏灯中出现红灯的数量为
，当这排装饰灯闪烁一次时：
（1）求
时的概率；（2）求的数学期望．
内，不等式
确定的平面区域为
，不等式组
确定的平面区域为
.
（1）定义横、纵坐标为整数的点为“整点”. 在区域中任取3个“整点”，求这些“整点”中恰好有2个“整点”落在区域中的概率；
（2）在区域中每次任取一个点，连续取3次，得到3个点，记这3个点落在区域中的个数为
，求的分布列和数学期望．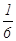
，第二轮检测不合格的概率为
，两轮检测是否合格相互没有影响。
（1）求该产品不能销售的概率
（2）如果产品可以销售，则每件产品可获利40元；如果产品不能销售，则每件产品亏损80元（即获利-80元）。已知一箱中有4件产品，记可销售的产品数为X，求X的分布列，并求一箱产品获利的均值。
（1）求这3名学生选修课所有选法的总数；
（2）求恰有2门选修课没有被这3名学生选择的概率；
（3）求A选修课被这3名学生选择的人数的数学期望.
（2）在男生甲被选中的情况下，求女生乙也被选中的概率；
（3）设所选3人中女生人数为
，求的分布列及数学期望。
表示将两件次品被全部检查或推断出来所需检查次数。
（I）求两件次品被全部检查或推断出来所需检查次数恰为4次的概率；
（II）求的分布列和数学期望。
同步练习册答案
版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号
的边长为2.
，且
，求事件：“
”的概率；
，求事件“
的面积均大于
”的概率.