
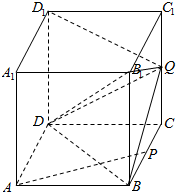
 如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.
如图,正方体ABCD-A1B1C1D1的棱长为2,P是BC的中点,点Q是棱CC1上的动点.分析 (1)延长AP交DC于M,连结D1M交C1C于点Q,根据相似三角形得出$\frac{CQ}{D{D}_{1}}$的比值,找出Q的位置;
(2)把△BB1Q当做棱锥的底面,则棱锥的高为DC,代入体积公式计算;
(3)连结AD1,则截面为等腰梯形APQD1,求出梯形的上下底和高,代入面积公式计算.
解答  解:(1)当Q是C1C中点时,直线D1Q,DC,AP交于一点.理由如下:
解:(1)当Q是C1C中点时,直线D1Q,DC,AP交于一点.理由如下:
延长AP交DC于M,连结D1M交C1C于点Q,∵CP∥AD,∴△MCP∽△MDA,∴$\frac{MC}{MD}=\frac{CP}{AD}=\frac{1}{2}$.
∵CQ∥D1D,∴△MCQ∽△MDD1,∴$\frac{CQ}{D{D}_{1}}$=$\frac{MC}{MD}=\frac{1}{2}$,∴Q是C1C中点.
(2)V${\;}_{棱锥{B}_{1}-DBQ}$=V${\;}_{棱锥D-B{B}_{1}Q}$=$\frac{1}{3}{S}_{△B{B}_{1}Q}$•CD=$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$.
(3)连结AD1,则过点A,P,Q三点的平面截正方体所得截面是梯形APQD1,
DD1=$\sqrt{2}AD$=2$\sqrt{2}$,PQ=$\frac{1}{2}A{D}_{1}$=$\sqrt{2}$,AP=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{5}$,QD1=$\sqrt{{D}_{1}{{C}_{1}}^{2}+Q{{C}_{1}}^{2}}$=$\sqrt{5}$.
∴梯形APQD1的高h=$\sqrt{A{P}^{2}-[\frac{1}{2}(A{D}_{1}-PQ)]{\;}^{2}}$=$\frac{3\sqrt{2}}{2}$.
∴S=$\frac{1}{2}$(PQ+AD1)•h=$\frac{9}{2}$.
点评 本题考查了平面的基本性质,棱锥的体积计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(20.7)<f(-log25)<f(-3) | B. | f(-3)<f(20.7)<f(-log25) | ||
| C. | f(-3)<f(-log25)<f(20.7) | D. | f(20.7)<f(-3)<f(-log25) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
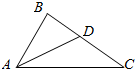 如图,在△ABC中,∠B=$\frac{π}{2}$,∠BAC的平分线交BC于点D,AD=$\sqrt{2}$,AC=$\sqrt{6}$,则△ABC的面积为$\frac{3\sqrt{3}}{4}$.
如图,在△ABC中,∠B=$\frac{π}{2}$,∠BAC的平分线交BC于点D,AD=$\sqrt{2}$,AC=$\sqrt{6}$,则△ABC的面积为$\frac{3\sqrt{3}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com