
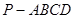 中,
中,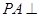 平面
平面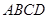 ,底面
,底面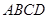 为矩形,
为矩形,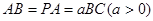 .
.
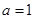 时,求证:
时,求证: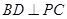 ;
;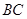 边上有且只有一个点
边上有且只有一个点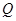 ,使得
,使得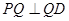 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值. 。
。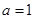 时,底面
时,底面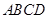 为正方形,
为正方形,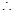
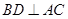
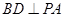 ,
,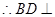 面
面 …………………………2分
…………………………2分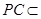 面
面
 …………………………3分
…………………………3分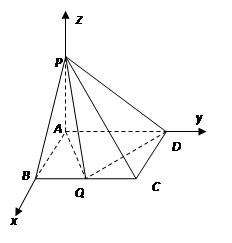
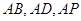 两两垂直,分别以它们所在直线
两两垂直,分别以它们所在直线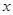 轴、
轴、 轴、
轴、 轴建立坐标系,如图所示,
轴建立坐标系,如图所示,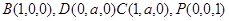 …………………4分
…………………4分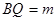 ,则
,则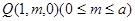
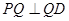 ,只要
,只要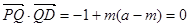
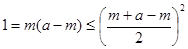 ,即
,即 ………6分
………6分 时,存在点
时,存在点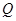 使得
使得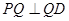
 ,即
,即 时,
时,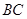 边上有且只有一个点
边上有且只有一个点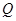 ,使得
,使得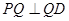
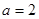 …………………………8分设面
…………………………8分设面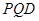 的法向量
的法向量
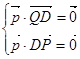 即
即 解得
解得 …………………………10分
…………………………10分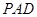 的法向量
的法向量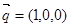
 的大小与二面角
的大小与二面角 的大小相等所以
的大小相等所以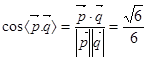
 的余弦值为
的余弦值为 …………………………12分
…………………………12分

科目:高中数学 来源:不详 题型:解答题
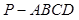 的底面
的底面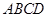 是正方形,侧棱
是正方形,侧棱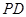 ⊥底面
⊥底面 ,
,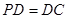 ,
, 是
是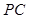 的中点.
的中点. 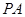 //平面
//平面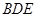 ;
; 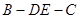 的平面角的余弦值;
的平面角的余弦值;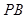 上是否存在点
上是否存在点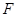 ,使
,使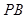 ⊥平面
⊥平面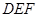 ?若存在,请求出
?若存在,请求出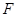 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
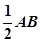 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.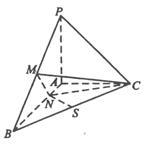
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
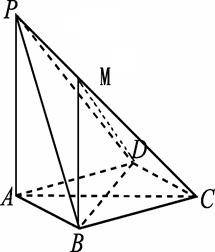
 与平面
与平面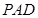 所成角的正切值;
所成角的正切值; ,CM=3,求二面角
,CM=3,求二面角 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
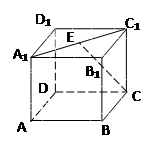
| A.直线AC | B.直线B1D1 |
| C.直线A1D1 | D.直线A1A |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, 是不同的平面,
是不同的平面, ,
, 是不同的直线,给出下列命题:
是不同的直线,给出下列命题: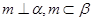 ,则
,则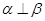 ;
;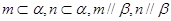 ,则
,则 ;
;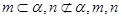 是异面直线,则
是异面直线,则 与
与 相交;
相交;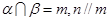 ,且
,且 ,则
,则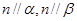 .
.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com