练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    点P(4，－2)与圆x2＋y2＝4上任一点连线的中点轨迹方程是

    A．(x－2)2＋(y＋1)2＝1           B．(x－2)2＋(y－1)2＝4

    C．(x－4)2＋(y－2)2＝1           D．(x－2)2＋(y－1)2＝1


     A、　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，在三棱柱ABC­A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB＝3，BC＝5.

    (1)求证：AA1⊥平面ABC；

    (2)求二面角A1­BC1­B1的余弦值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     若{ an} 是各项均不为零的等差数列, 公差为d, Sn 为其前n 项和, 且满足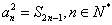。数列{ bn} 满足 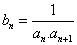为数列{ bn} 的前n项和。

    （Ⅰ） 求an 和Tn;

    （Ⅱ） 是否存在正整数 m、 n（ 1<m<n） , 使得T1、 Tm、 Tn 成等比数列? 若存在, 求出所有

    m、 n的值; 若不存在, 请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在底面是正方形的四棱锥中，，，点在上，且.

    （Ⅰ）求证：平面；

    （Ⅱ）求二面角的余弦值；

    （Ⅲ）在棱上是否存在一点，使得平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是

    A．若m∥α，n∥α，则m∥n          

    B．若α⊥γ，β⊥γ，则α∥β

    C．若m∥α，m∥β，则α∥β          

    D．若m⊥α，n⊥α，则m∥n

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆C过点(1,0)，且圆心在x轴的正半轴上，直线l：y＝x－1被圆C所截得的弦长为2，则过圆心且与直线l垂直的直线的方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设是两个非空集合，定义运算，已知，，则       （   ）

    A.         B.           C.        D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得分）。设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立。

    （1）设每盘游戏获得的分数为，求的分布列；

    （2）玩三盘游戏，至少有一盘出现音乐的概率是多少？

    （3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了。请运用概率统计的相关知识分析分数减少的原因。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知

    （1）求函数的最小正周期和函数在上的单调减区间；

    （2）若中，，求角.

    查看答案和解析>>

    同步练习册答案