解:(1)当n=1时,a
1=1
当n=2时,S
2=2,∴a
2=S
2-a
1=1…(2分)
当n≥3时,a
n=S
n-S
n-1=2n-4
∴
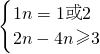
…(6分)
(2)①当m=1时a
1=1,a
2=1,a
3=2不能成等比数列…(8分)
②当m=2时a
2=1,a
3=2,a
4=4,成等比数列…(10分)
③当m≥3时,若a
m,a
m+1,a
m+2成等比数列,
则a
m•a
m+2=a
m+12即(2m-4)•2m=(2m-2)
2 得4=0矛盾,不可能成立 …(9分)
综上所述,得存在m=2使得a
m,a
m+1,a
m+2成等比数列…(14分)
分析:(1)根据题中给出的式子先求出当n=1和n=2时,a
n的表达式,再用公式求出当n≥3时,a
n=S
n-S
n-1=2n-4,最后综合可得数列{a
n}的通项公式;
(2)首先根据m=1和m=2验证a
m,a
m+1,a
m+2成等比数列是否成立,然后讨论当m≥3时,假设a
m,a
m+1,a
m+2成等比数列成立,用等比中项列式列式,得到矛盾,从而说明m≥3时a
m,a
m+1,a
m+2成等比数列不成立.最后综合可得正确结论.
点评:本题考查了数列的通项与求和公式,以及等比中项的概念,考查了分类讨论的数学思想,属于中档题.


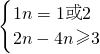 …(6分)
…(6分)
