
定义在[﹣1,1]上的奇函数f(x)满足f(1)=2,且当a,b∈[﹣1,1],a+b≠0时,有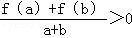 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若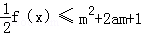 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
(1)详见解析;(2)
解析试题分析:(1)假设函数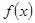 的图象上存在两个不同的点
的图象上存在两个不同的点 ,使直线
,使直线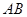 恰好与
恰好与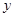 轴垂直,设
轴垂直,设 的横坐标为
的横坐标为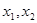 ,且
,且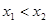 ,然后证得
,然后证得 ;推出函数
;推出函数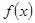 在
在 上是增函数,这与这与
上是增函数,这与这与 假设矛盾,可得假设不成立,命题得证.
假设矛盾,可得假设不成立,命题得证.
(2)由题意可得函数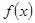 的最大值小于或等于
的最大值小于或等于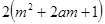 ,结合(1)的过程,可求出其最大值
,结合(1)的过程,可求出其最大值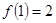 ,即整理的:
,即整理的: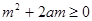 .令关于
.令关于 的一次函数
的一次函数 g(a)=m2+2am,则有
g(a)=m2+2am,则有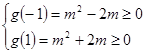 ,由此求得m的范围.
,由此求得m的范围.
考点:1.反证法;2.函数的恒成立问题.试题解析:解:(1)假设函数f(x)的图象上存在两个不同的点A,B,使直线AB恰好与y轴垂直,
则A、B两点的纵坐标相同,设它们的横坐标分别为 x1和x2,且x1<x2.
则f(x1)﹣f(x2)=f(x1)+f(﹣x2)=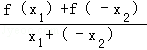 [x1+(﹣x2)].
[x1+(﹣x2)].
由于 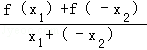 >0,且[x1+(﹣x2)]<0,∴f(x1)﹣f(x2)<0,
>0,且[x1+(﹣x2)]<0,∴f(x1)﹣f(x2)<0,
故函数f(x)在[﹣1,1]上是增函数.
这与假设矛盾,故假设不成立,即 函数f(x)的图象上不存在两个不同的点A,B,使直线AB恰好与y轴垂直.
(2)由于  对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,
∴故函数f(x)的最大值小于或等于2(m2+2am+1).
由于由(1)可得,函数f(x)是[﹣1,1]的增函数,故函数f(x)的最大值为f(1)=2,
∴2(m2+2am+1)≥2,即 m2+2am≥0.
令关于a的一次函数g(a)=m2+2am,则有  ,
,
解得 m≤﹣2,或m≥2,或 m=0,故所求的m的范围是{m|m≤﹣2,或m≥2,或 m=0}.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度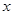 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当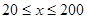 时,车流速度
时,车流速度 是车流密度
是车流密度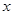 的一次函数.
的一次函数.
(1)当 时,求函数
时,求函数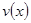 的表达式;
的表达式;
(2)当车流密度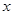 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)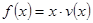 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本 (万元)可以看成月产量
(万元)可以看成月产量 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本 (万元)关于月产量
(万元)关于月产量 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: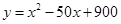 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为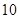 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴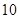 万元.
万元.
(1)当 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)= 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设x1、x2是关于x的方程f(x)= 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com