
【题目】已知函数![]() (其中
(其中![]() 是常数,且
是常数,且![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然对数的底),使得
是自然对数的底),使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]()
【解析】
(1)求出![]() 在
在![]() 处的导数,利用斜率和函数值建立等式关系,则可求出
处的导数,利用斜率和函数值建立等式关系,则可求出![]() 的值. (2)由条件可知,原题等价于
的值. (2)由条件可知,原题等价于![]() 在
在![]() 上有解,设
上有解,设![]() ,即
,即![]() ,求导求函数的最值,从而求出
,求导求函数的最值,从而求出![]() 的取值范围. (3)通过求导分析
的取值范围. (3)通过求导分析![]() 的单调性和最值,分类讨论求出
的单调性和最值,分类讨论求出![]() 的取值范围.
的取值范围.
(1)![]() ,由题知
,由题知![]() ,且
,且![]() ,
,
解得![]() ;
;
(2)由(1)知![]() ,因为存在
,因为存在![]() ,使得
,使得![]() ,
,
即![]() ,设
,设![]() ,则需
,则需![]() ,
,
![]() ,设
,设![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 单调递增,又因为
单调递增,又因为![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 单调递增,所以
单调递增,所以![]() ,
,
令![]() ,解得
,解得![]() ;
;
(3)![]() ,
,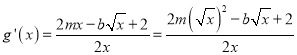 ,
,
①当![]() 时,对任意
时,对任意![]() ,易知方程
,易知方程![]() 均仅有唯一解
均仅有唯一解![]() ,
,
且当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
故方程![]() 最多有两个不同的实数解,所以
最多有两个不同的实数解,所以![]() 不符合题意;
不符合题意;
② 当![]() 时,若
时,若![]() ,则
,则![]() 恒成立,
恒成立,![]() 单调递增,
单调递增,
方程![]() 最多只有一个实数解,不符题意,
最多只有一个实数解,不符题意,
所以对任意![]() ,应有
,应有![]() ,即
,即![]() ,
,
此时,易知方程![]() 在
在![]() 上有两个不同的实数根
上有两个不同的实数根![]() ,
,
因为![]() ,不妨取
,不妨取![]() ,则有
,则有![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
由表可知,![]() 的极大值为
的极大值为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为![]() ,且
,且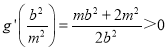 ,所以
,所以![]() ,
,
因为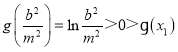 ,所以必然存在
,所以必然存在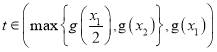 ,
,
使得方程![]() 在区间
在区间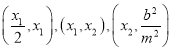 上均有一个实数解,符合题意;
上均有一个实数解,符合题意;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:PA//平面BEF;
(Ⅱ)若PC与AB所成角为![]() ,求
,求![]() 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年全球爆发新冠肺炎,人感染了新冠肺炎病毒后常见的呼吸道症状有:发热、咳嗽、气促和呼吸困难等,严重时会危及生命.随着疫情的发展,自2020年2月5日起,武汉大面积的爆发新冠肺炎,政府为了及时收治轻症感染的群众,逐步建立起了14家方舱医院,其中武汉体育中心方舱医院从2月12日开舱至3月8日闭仓,累计收治轻症患者1056人.据部分统计该方舱医院从2月26日至3月2日轻症患者治愈出仓人数的频数表与散点图如下:
日期 | 2.26 | 2.27 | 2.28 | 2.29 | 3.1 | 3.2 |
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
出仓人数 | 3 | 8 | 17 | 31 | 68 | 168 |

根据散点图和表中数据,某研究人员对出仓人数![]() 与日期序号
与日期序号![]() 进行了拟合分析.从散点图观察可得,研究人员分别用两种函数①
进行了拟合分析.从散点图观察可得,研究人员分别用两种函数①![]() ②
②![]() 分析其拟合效果.其相关指数
分析其拟合效果.其相关指数![]() 可以判断拟合效果,R2越大拟合效果越好.已知
可以判断拟合效果,R2越大拟合效果越好.已知![]() 的相关指数为
的相关指数为![]() .
.
(1)试根据相关指数判断.上述两类函数,哪一类函数的拟合效果更好?(注:相关系数![]() 与相关指数R2满足
与相关指数R2满足![]() ,参考数据表中
,参考数据表中![]() )
)
(2)①根据(1)中结论,求拟合效果更好的函数解析式;(结果保留小数点后三位)
②3月3日实际总出仓人数为216人,按①中的回归模型计算,差距有多少人?
(附:对于一组数据![]() ,其回归直线为
,其回归直线为![]()
相关系数
参考数据:
|
|
|
|
|
|
|
|
|
3.5 | 49.17 | 15.17 | 3.13 | 894.83 | 19666.83 | 10.55 | 13.56 | 3957083 |
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,试问:
,试问:![]() 是否与平面
是否与平面![]() 平行?若平行,求三棱锥
平行?若平行,求三棱锥![]() 的体积;若不平行,请说明理由.
的体积;若不平行,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是等差数列,数列
是等差数列,数列![]() 是等比数列,且
是等比数列,且![]() ,
,![]() 的前n项和为
的前n项和为![]() .若
.若![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足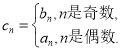 问:是否存在正整数
问:是否存在正整数![]() ,使得
,使得![]() ,若存在求出
,若存在求出![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若存在各项均为正整数公差为![]() 的无穷等差数列
的无穷等差数列![]() ,满足
,满足![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() 成等比数列,求
成等比数列,求![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度,某地区在2015年以前的年均脱贫率(脱贫的户数占当年贫困户总数的比)为70%,2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加户数占2019年贫困总户数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 |
参加占户比 | 45% | 45% | 10% |
脱贫率 | 96% | 96% | 90% |
那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】垃圾分类,是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而转变成公共资源的一系列活动的总称.分类的目的是提高垃圾的资源价值和经济价值,力争物尽其用.2019年6月25日,生活垃圾分类制度入法.到2020年底,先行先试的46个重点城市,要基本建成垃圾分类处理系统;其他地级城市实现公共机构生活垃圾分类全覆盖.某机构欲组建一个有关“垃圾分类”相关事宜的项目组,对各个地区“垃圾分类”的处理模式进行相关报道.该机构从600名员工中进行筛选,筛选方法:每位员工测试![]() ,
,![]() ,
,![]() 三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试
三项工作,3项测试中至少2项测试“不合格”的员工,将被认定为“暂定”,有且只有一项测试“不合格”的员工将再测试![]() ,
,![]() 两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试
两项,如果这两项中有1项以上(含1项)测试“不合格”,将也被认定为“暂定”,每位员工测试![]() ,
,![]() ,
,![]() 三项工作相互独立,每一项测试“不合格”的概率均为
三项工作相互独立,每一项测试“不合格”的概率均为![]() .
.
(1)记某位员工被认定为“暂定”的概率为![]() ,求
,求![]() ;
;
(2)每位员工不需要重新测试的费用为90元,需要重新测试的总费用为150元,除测试费用外,其他费用总计为1万元,若该机构的预算为8万元,且该600名员工全部参与测试,问上述方案是否会超过预算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网金融的不断发展,很多互联网公司推出余额增值服务产品和活期资金管理服务产品,如蚂蚁金服旗下的“余额宝”,腾讯旗下的“财富通”,京东旗下“京东小金库”.为了调查广大市民理财产品的选择情况,随机抽取1100名使用理财产品的市民,按照使用理财产品的情况统计得到如下频数分布表:
分组 | 频数(单位:名) |
使用“余额宝” |
|
使用“财富通” |
|
使用“京东小金库” | 40 |
使用其他理财产品 | 60 |
合计 | 1100 |
已知这1100名市民中,使用“余额宝”的人比使用“财富通”的人多200名.
(1)求频数分布表中![]() ,
,![]() 的值;
的值;
(2)已知2018年“余额宝”的平均年化收益率为![]() ,“财富通”的平均年化收益率为
,“财富通”的平均年化收益率为![]() ,“京东小金库”的平均年化收益率为
,“京东小金库”的平均年化收益率为![]() ,有3名市民,每个人理财的资金有10000元,且分别存入“余额宝”“财富通”“京东小金库”,求这3名市民2018年理财的平均年化收益率;
,有3名市民,每个人理财的资金有10000元,且分别存入“余额宝”“财富通”“京东小金库”,求这3名市民2018年理财的平均年化收益率;
(3)若在1100名使用理财产品的市民中,从使用“余额宝”和使用“财富通”的市民中按分组用分层抽样方法共抽取5人,然后从这5人中随机选取2人,求“这2人都使用‘财富通’”的概率.
注:平均年化收益率,也就是我们所熟知的利率,理财产品“平均年化收益率为![]() ”即将100元钱存入某理财产品,一年可以获得3元利息.
”即将100元钱存入某理财产品,一年可以获得3元利息.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P恒过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆P圆心的轨迹M的方程;
(Ⅱ)正方形ABCD中,一条边AB在直线y=x+4上,另外两点C、D在轨迹M上,求正方形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com