
【题目】已知向量m=(cosx,-1),n=![]() ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.
(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=1,c=![]() ,且f(A)恰是函数f(x)在
,且f(A)恰是函数f(x)在![]() 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂36名工人的年龄数据如下表.
工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 | 工人编号 年龄 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值x和方差s2;
(3)36名工人中年龄在![]() 与
与![]() 之间有多少人?所占的百分比是多少(精确到0.01%)?
之间有多少人?所占的百分比是多少(精确到0.01%)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 |
y(万盒) | 4 | 4 | 5 | 6 | 6 |
(1)该同学为了求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出![]() =0.6,试求出
=0.6,试求出![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题,记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 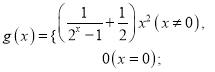
![]() ;
; ![]() . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是![]() ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为![]() 的正方形.
的正方形.
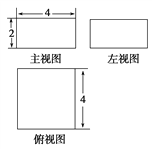
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com