解:(1)将函数化简,得:
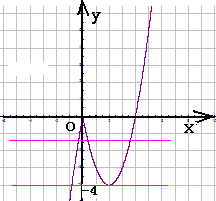
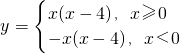
∴当x≥0时,图象取开口向上的抛物线的y轴右侧,
当x<0时,图象取开口向下的抛物线左侧
所得图象如右图 …
(2)在同一坐标系里作出直线y=k,它是一条与x轴平行的直线,
再根据k值的变化,来观察观察它与函数y=f(x)图象公共点的个数:
①当k>0或k<-4时,直线y=k与函数y=f(x)图象有唯一公共点
∴当k>0或k<-4时,方程|x|•(x-4)=k有一解 …
②当k=0或k=-4时,直线y=k与函数y=f(x)图象有两个公共点
∴k=0或k=-4时,方程|x|•(x-4)=k有两解 …
③当-4<k<0时,直线y=k与函数y=f(x)图象有三个公共点
∴当-4<k<0时,方程|x|•(x-4)=k有三解 …
综上所述:当k>0或k<-4时,原方程有一解;当k=0或k=-4时,原方程有两解;当-4<k<0时,原方程有三解.
分析:(1)根据绝对值的意义将函数去绝对值,化简为
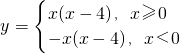
,再分x≥0与x<0两部分对所作的抛物线进行截取,可得符合题意的图象;
(2)同一坐标系里作出y=f(x)与y=k的图象,然后根据k值的变化观察两图象的交点的个数,可得原方程解的个数,最后综合可回答提出的问题.
点评:本题考查了函数的图象与性质、函数图象的作法等知识点,属于中档题.遇到绝对值问题,根据定义去绝对值,是解题的常用思路,解题过程中还要注意分类讨论及最后的综合等细节.


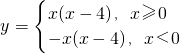
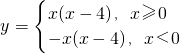 ,再分x≥0与x<0两部分对所作的抛物线进行截取,可得符合题意的图象;
,再分x≥0与x<0两部分对所作的抛物线进行截取,可得符合题意的图象;

 已知函数f(x)=
已知函数f(x)= 已知f(x)=
已知f(x)=