Question

已知f(x)=

x2+2|x|

x+2

，g(x)=

x+2

，H（x）=f（x）•g（x）．
（1）画出函数y=H（x-1）+2的图象；
（2）试讨论方程H（x-1）+2=m根的个数．

Answer 1

分析：（1）根据表达式，得出函数f（x）的定义域是（-2，+∞），将H（x）化成分段函数的形式．从而得出函数y=H（x-1）+2的分段表达式，进而可以作出它的图象；
（2）根据图象可以得到，当m=2或m≥10时，直线y=m与函数y=H（x-1）+2图象有且仅有一个公共点；当2＜m＜10时，直线y=m与函数y=H（x-1）+2图象有两个公共点；当m＜2时，直线y=m与函数y=H（x-1）+2图象没有公共点．由此则不难得出方程根的个数了．

解答：解：（1）H（x）的定义域为{x|x＞-2}
H(x)=x2+2|x|=

x2+2x(x≥0) x2-2x(-2＜x＜0)

y=H（x-1）+2=(x-1)2+2|x-1|+2=

x2+1(x≥1) x2-4x+5(-1＜x＜1)

图象如下：

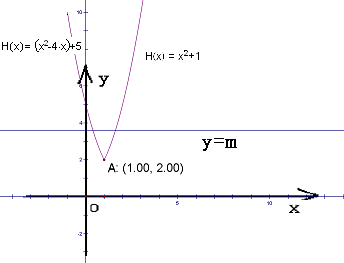
（2）在同一坐标系里作出直线y=m，观察它与函数y=H（x）图象的交点的个数，可得
①当m=2或m≥10时，直线y=m与函数y=H（x-1）+2图象有且仅有一个公共点；②当2＜m＜10时，直线y=m与函数y=H（x-1）+2图象有两个公共点；③当m＜2时，直线y=m与函数y=H（x-1）+2图象没有一个公共点
由此可得：当m∈{2}∪[10，+∞）时，方程H（x-1）+2=m有且仅有一个实数根；
当m∈[2，10）时，方程H（x-1）+2=m有且仅有两个实数根；
当m∈（-∞，2）时，方程H（x-1）+2=m有0个实数根．

点评：本题考查了函数的图象与根的分布等等知识点，属于中档题．利用图象观察，得到方程根的个数，是数学常用的思想方法，也是这类问题的常用解法．