
(12分)已知椭圆E的两个焦点分别为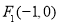 和
和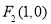 ,离心率
,离心率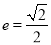 .
.
(1)求椭圆E的方程;
(2)设直线 与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
(1)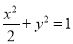 ,(2)
,(2)
【解析】
试题分析:(1)由题意可知椭圆中已知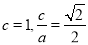 ,以及
,以及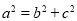 ,即可求得
,即可求得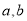 ,即可求出椭圆的标准方程.
,即可求出椭圆的标准方程.
(2)依题意可得联立直线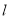 与椭圆E的方程消去y,即可得到一个关于x的方程,由
与椭圆E的方程消去y,即可得到一个关于x的方程,由 ,可得m的取值范围.再结合韦达定理写出AB中点的坐标,再写出线段AB的垂直平分线,并写出点T的坐标.由弦长公式以及点到直线的距离公式即可得到三角形的面积公式,再根据二次函数最值的求法,即可求出结论.
,可得m的取值范围.再结合韦达定理写出AB中点的坐标,再写出线段AB的垂直平分线,并写出点T的坐标.由弦长公式以及点到直线的距离公式即可得到三角形的面积公式,再根据二次函数最值的求法,即可求出结论.
试题解析:(1)根据题意得 解得
解得 2分
2分
 所求椭圆方程为
所求椭圆方程为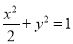 4分
4分
(2)【解析】
设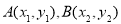
连立方程组
化简得: 6分
6分
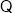 有两个不同的交点
有两个不同的交点

即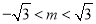 且
且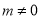
由根与系数的关系得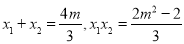
设A、B中点为C,C点横坐标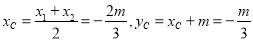
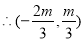
 线段AB垂直平分线方程为
线段AB垂直平分线方程为
 T点坐标为
T点坐标为
T到AB的距离 8分
8分
由弦长公式得 10分
10分



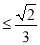
当 即
即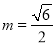
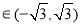 时等号成立
时等号成立
 12分
12分
考点:1.椭圆的标准方程.2.直线与椭圆的位置关系.3.最值问题.


科目:高中数学 来源:2015届河北省石家庄市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知盒中装有3个红球、2个白球、5个黑球,它们大小形状完全相同,现需一个红球,甲每次从中任取一个不放回,在他第一次拿到白球的条件下,第二次拿到红球的概率( ).
A.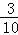 B.
B. C.
C.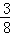 D.
D.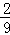
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
若抛物线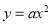 的准线的方程是
的准线的方程是 ,则实数a的值是( )
,则实数a的值是( )
A. B.
B. C.8 D.
C.8 D.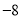
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考文科数学试卷(解析版) 题型:填空题
在下列给出的命题中,所有正确命题的序号为 .
①函数 的图象关于点
的图象关于点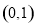 成中心对称;
成中心对称;
②对 若
若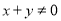 ,则
,则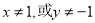 ;
;
③若实数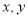 满足
满足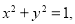 则
则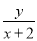 的最大值为
的最大值为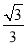 ;
;
④若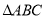 为钝角三角形,则
为钝角三角形,则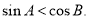
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考文科数学试卷(解析版) 题型:选择题
已知向量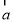 ,
,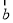 的夹角为45°,且
的夹角为45°,且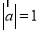 ,
,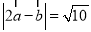 ,则
,则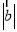 =( )
=( )
A. B.
B. C.
C.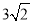 D.
D.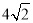
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:解答题
(1)求 的值.
的值.
(2)已知6 sin2x+sinxcosx-2cos2x=0,π<x<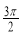 ,试求sin2x-cos2x+tan2x的值.
,试求sin2x-cos2x+tan2x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com