
分析 (1)利用绝对值的几何意义,写出分段函数,即可解f(x)>2的解集;
(Ⅱ)先用绝对值三角不等式将问题等价为:f(x)min=|a||≥a2-3a-3,再分类讨论求解即可.
解答 解:(Ⅰ)当a=1时,f(x)=|x-1|+|x-2|.
x≤1时,f(x)=-x+1-x+2=3-2x,由不等式f(x)>2可得x<$\frac{1}{2}$;
1<x<2时,f(x)=x-1-x+2=1由不等式f(x)>2可得x∈∅;
x≥2时,f(x)=x-1+x-2=2x-3,由不等式f(x)>2可得x>$\frac{5}{2}$;
∴不等式f(x)>2的解集为(-∞,$\frac{1}{2}$)∪($\frac{5}{2}$,+∞);
(Ⅱ)因为不等式f(x)≥a2-3a-3对x∈R恒成立,
所以,f(x)min≥a2-3a-3,
根据绝对值三角不等式,|x-a|+|x-2a|≥|(x-a)-(x-2a)|=|a|,
即f(x)min=|a|,所以,|a||≥a2-3a-3,分类讨论如下:
①当a≥0时,a≥a2-3a-3,即a2-4a-3≤0,∴2-$\sqrt{7}$≤a≤2+$\sqrt{7}$,此时0≤a≤2+$\sqrt{7}$;
②当a<0时,-a≥a2-3a-3,即a2-2a-3≤0,∴-1≤a≤3,此时-1≤a<0.
综合以上讨论得,实数a的取值范围为:[-1,2+$\sqrt{7}$].
点评 本题主要考查函数的恒成立问题,绝对值不等式的解法,关键是去掉绝对值,化为与之等价的不等式组来解,体现了分类讨论、转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
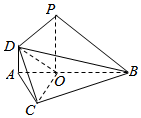 如图$∠ABC=\frac{π}{4},O$为AB上一点,且3OB=3OC=2AB,又PO⊥平面ABC,2DA=2AO=PO,且DA∥PO.
如图$∠ABC=\frac{π}{4},O$为AB上一点,且3OB=3OC=2AB,又PO⊥平面ABC,2DA=2AO=PO,且DA∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (-$\frac{2}{3}$,1) | D. | (-∞,-$\frac{2}{3}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin|x| | B. | y=cos|x| | C. | y=$\frac{1}{|tanx|}$ | D. | y=lg|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com