
分析 (1)根据题意,对x分3种情况讨论:①当x<0时,②当0≤x<$\frac{1}{2}$时,③当x≥$\frac{1}{2}$时;在各种情况下.去掉绝对值,化为整式不等式,解可得三个解集,进而将这三个解集取并集即得所求.
(2)根据|f(x)-f(a)|=|x2-x-a2+a|=|x-a|•|x+a-1|<|x+a-1|=|x-a+2a-1|≤|x-a|+|2a-1|<1+|2a|+1,证得结果.
解答 (1)解:根据题意,对x分3种情况讨论:
①当x<0时,原不等式可化为-2x+1<-x+1,解得x>0,又x<0,则x不存在,
此时,不等式的解集为∅.
②当0≤x<$\frac{1}{2}$时,原不等式可化为-2x+1<x+1,解得x>0,又0≤x<$\frac{1}{2}$,
此时其解集为{x|0<x<$\frac{1}{2}$}.
③当x≥$\frac{1}{2}$时,原不等式化为2x-1<x+1,解得$\frac{1}{2}$≤x<2,
又由x≥$\frac{1}{2}$,此时其解集为{x|$\frac{1}{2}$≤x<2},
综上,原不等式的解集为{x|0<x<2}.
(2)证明:∵f(x)=x2-x+1,实数a满足|x-a|<1,
故|f(x)-f(a)|=|x2-x-a2+a|=|x-a|•|x+a-1|<|x+a-1|=|x-a+2a-1|≤|x-a|+|2a-1|<1+|2a|+1=2(|a|+1).
∴|f(x)-f(a)|<2(|a|+1).
点评 本题主要考查绝对值不等式的解法,绝对值不等式的性质,用放缩法证明不等式,体现了分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
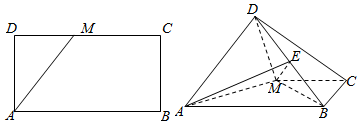
 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com