
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
| 分组 | 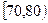 | 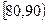 | 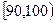 |  | 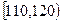 | 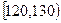 | 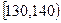 | [140,150] |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | 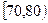 | 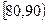 | 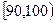 |  | 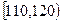 | 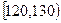 | 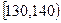 | [140,150] |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
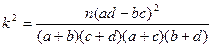
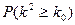 | 0.10 | 0.025 | 0.010 |
 | 2.706 | 5.024 | 6.635 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
某工厂2010年第三季度生产的A,B,C,D四种型号的产品产量用条形图形表示如图,现用分层抽样的方法从中选取50件样品参加2011年4月份的一个展销会。
(1)A,B,C,D型号的产品各抽取多少件?
(2)从50件样品随机地抽取2件,求这2件产品恰好是不同型号产品的概率。
(3)从A,C型号的样品中随机地抽取3件,用ξ表示抽取A型号的产品件数,求ξ的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一机器可以按各种不同速度运转,其生产的产品有一些会有缺点,每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据:
| 速度(x转/秒) |
| ||
| 8 | 6 | ||
| 9 | 8 | ||
| 10 | 10 | ||
| 13 | 12 |
 用分数表示)
用分数表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润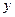 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 | 2 | 3 | 4 | 5 |
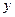 | 18 | 27 | 32 | 35 |
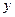 关于
关于 的线性回归方程
的线性回归方程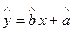 ;
;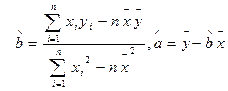
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| | 甲 | 乙 | 丙 |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校组织一次篮球投篮测试,已知甲同学每次投篮的命中率均为1/2。
(1)若规定每投进1球得2分,甲同学投篮4次,求总得分X的概率分布和数学期望。
(2)假设连续3次投篮未中或累计7次投篮未中,则停止投篮测试,问:甲同学恰好投篮10次,被停 止投篮测试的概率是多少?
止投篮测试的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分) 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整 数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
 60.5~70.5 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 50 | |
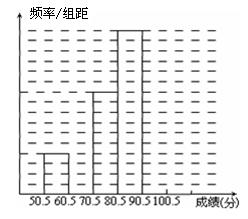

 补全频率分布直方图;
补全频率分布直方图;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
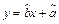 ;
;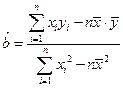 ,
,
 100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com