练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据

    ｘ
    		３
    		４
    		５
    		６
    ｙ
    		２．５
    		３
    		４
    		４．５
    （１） 请画出上表数据的散点图；
    （２） 请根据上表提供的数据，用最小二乘法求出ｙ关于ｘ的线性回归方程；
    （附：最小二乘法求线性回归方程系数公式 ，
    另外：计算数据3×2．5+4×3+5×4+6×4.5=66.5可供使用）
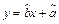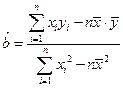    （３） 已知该厂技术改造前１００吨甲产品能耗为９０吨标准煤；试根据（２）所求出的线性回归方程，预测生产１００吨甲产品的生产能耗比技术改造前降低多少吨标准煤？



    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    甲乙两个学校高三年级分别为1100人，1000人，为了统计两个学校在地区二模考试的数学科目成绩，采用分层抽样抽取了105名学生的成绩，并作出了部分频率分布表如下：（规定考试成绩在[120，150]内为优秀）
    甲校：

    分组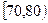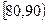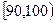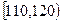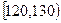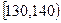







    		[140,150]
    频数
    		2
    		3
    		10
    		15
    		15
    		x
    		3
    		1
    乙校：
    分组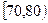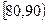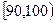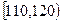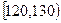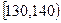







    		[140,150]
    频数
    		1
    		2
    		9
    		8
    		10
    		10
    		y
    		3
      （1）计算x，y的值，并分别估计两上学校数学成绩的优秀率；
    （2）由以上统计数据填写下面2×2列联表，并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
     
    		甲校
    		乙校
    		总计
    优秀
    		 
    		 
    		 
    非优秀
    		 
    		 
    		 
    总计
    		 
    		 
    		 
    附：

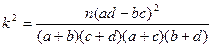
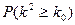    		0．10
    		0．025
    		0．010

    		2．706
    		5．024
    		6．635

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）某学校共有高一、高二、高三学生名，各年级男、女生人数如下图：

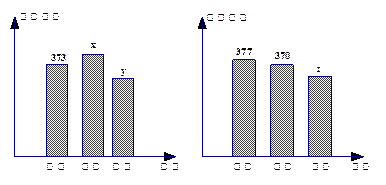
    已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0． 19．
    （Ⅰ）求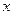的值；
    （Ⅱ）现用分层抽样的方法在全校抽取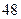名学生，问应在高三年级抽取多少名？
    （Ⅲ）已知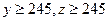，求高三年级中女生比男生多的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题12分）根据空气质量指数API（为整数）的不同，可将空气质量分级如下表：


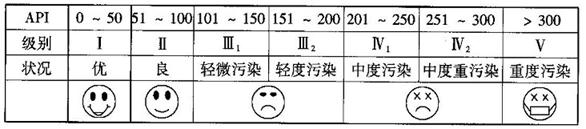
    对某城市一年（365天）的空气质量进行监测，获得的API数据按照区间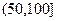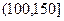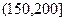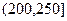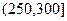，，，，，进行分组，得到频率分布直方图如图.                         
    （1）求直方图中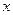的值；
    （2）计算一年中空气质量为良的天数；
    （3）某环保部门准备在一年内随机到该城市考察两次空气质量，求两次考察空气质量都为良的概率（结果用分数表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某班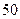名学生在一次百米测试中，成绩全部介于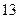秒与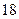秒之间，将测试结果按如下方式分成五组：第一组，第二组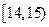，…，第五组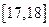，下图是按上述分组方法得到的频率分布直方图。
    （1）若成绩大于或等于秒且小于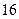秒认为良好，求该班在这次百米测试中成绩良好的人数；
    （2）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于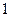的概率。

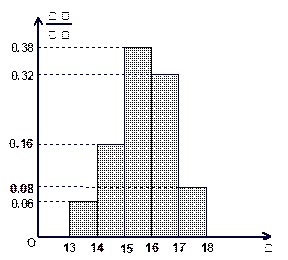
    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    已知某单位有50名职工，从中按系统抽样抽取10名职工，分别统计这10名职工的体重（单位：公斤），获得体重数据的茎叶图如图所示。
    （Ⅰ）求该样本的方差；
    （Ⅱ）从这10名职工中随机抽取两名体重不轻于73公斤的职工，求体重为76公斤的职工被抽取到的概率。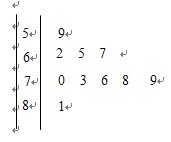

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （满分13分）某项实验，在100次实验中成功率只有10％，进行技术改造后，又进行了100次实验，若要有97．5％以上的把握认为“技术改造效果明显”，实验的成功率最小应是多少？（设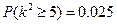,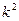的观测值为）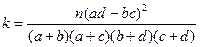
    （解答过程须列出列联表）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）已知x，y之间的一组数据如下表： 

    x
    		1
    		3
    		6
    		7
    		8
    y
    		1
    		2
    		3
    		4
    		5
    （1）以x为横坐标，y为纵坐标在直角坐标系中画出散点图，并说明这两个变量之间的关系是正相关关系还是负相关关系。
    （2）求线性回归方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）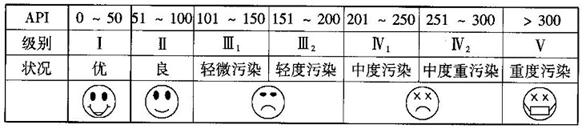

    根据空气质量指数API（为整数）的不同，可将空气质量分级如下表：
    对某城市一年（365天）的空气质量进行监测，获得的API数据按照区间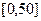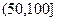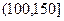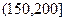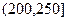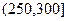，，，，，进行分组，得到频率分布直方图如图5.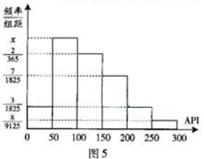                          
    （1）求直方图中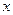的值；
    （2）计算一年中空气质量分别为良和轻微污染的天数；
    （3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率.
    （结果用分数表示．已知，， ，）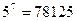

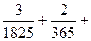
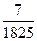
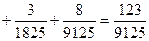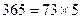    查看答案和解析>>

    同步练习册答案