
 在正方体AC1中.
在正方体AC1中.分析 (1)推导出AA1⊥底面ABCD,从而平面A1ADD1⊥平面ABCD,由此能求出平面A1ADD1与平面ABCD所成的二面角的大小.
(2)推导出AB⊥BC,AB⊥BC1,从而∠CBC1是平面ABC1D1与平面ABCD所成的二面角的平面角,由此能求出平面ABC1D1与平面ABCD所成的二面角的度数.
解答 解:(1)∵ 在正方体AC1中,AA1⊥AD,AA1⊥AB,AD∩AB=A,
在正方体AC1中,AA1⊥AD,AA1⊥AB,AD∩AB=A,
∴AA1⊥底面ABCD,
∵AA1?A1ADD1,∴平面A1ADD1⊥平面ABCD,
∴平面A1ADD1与平面ABCD所成的二面角为90°.
(2)∵在正方体AC1中,AB⊥平面BCC1B1,
∴AB⊥BC,AB⊥BC1,
∴∠CBC1是平面ABC1D1与平面ABCD所成的二面角的平面角,
∵BC=CC1,BC⊥CC1,
∴∠CBC1=45°,
∴平面ABC1D1与平面ABCD所成的二面角的度数为45°.
点评 本题考查二面角的求法,是基础题,解题时要认真审题,注意正方体结构特征的合理运用.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,其中正视图是圆心角为270°的扇形,俯视图与侧视图中圆的半径为2,则这个几何体的表面积是( )
一个几何体的三视图如图所示,其中正视图是圆心角为270°的扇形,俯视图与侧视图中圆的半径为2,则这个几何体的表面积是( )| A. | 16π | B. | 14π | C. | 12π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
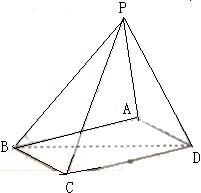 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,二面角A-PB-C为90°,PA=AB=2BC.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,二面角A-PB-C为90°,PA=AB=2BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
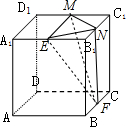 如图,在正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1和B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E,F,M,N分别是A1B1,BC,C1D1和B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
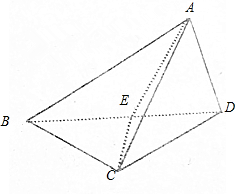 如图,在四面体ABCD中,CB=CD,AD⊥平面BCD,且E是BD的中点,求证:
如图,在四面体ABCD中,CB=CD,AD⊥平面BCD,且E是BD的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了调查某地区成年人血液的一项指标,现随机抽取了成年男性、女性各10人组成的一个样本,对他们的这项血液指标进行了检测,得到了如下茎叶图.根据医学知识,我们认为此项指标大于40为偏高,反之即为正常.
为了调查某地区成年人血液的一项指标,现随机抽取了成年男性、女性各10人组成的一个样本,对他们的这项血液指标进行了检测,得到了如下茎叶图.根据医学知识,我们认为此项指标大于40为偏高,反之即为正常.| 正常 | 偏高 | 合计 | |
| 男性 | |||
| 女性 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com