已知非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},
(Ⅰ)当a=10时,求A∩B,A∪B;
(Ⅱ)求能使A⊆(A∩B)成立的a的取值范围.
【答案】
分析:(Ⅰ)当a=10时,A={21≤x≤25},B={x|3≤x≤22},由此能求出A∩B和A∪B.
(Ⅱ)由A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},且A⊆(A∩B),知
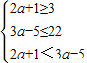
,由此能求出a的取值范围.
解答:解:(Ⅰ)当a=10时,A={21≤x≤25},B={x|3≤x≤22},
∴A∩B={x|21≤x≤22},
A∪B={x|3≤x≤25}.
(Ⅱ)∵A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},
且A⊆(A∩B),
∴
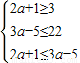
,
解得6≤a≤9.
∴a的取值范围是[6,9].
点评:本题考查集合的交、并、补集的混合运算,是基础题.解题时要认真审题,仔细解答.

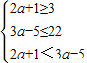 ,由此能求出a的取值范围.
,由此能求出a的取值范围.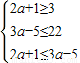 ,
,

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案