
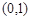 上产生两个随机数
上产生两个随机数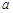 和
和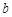 ,则方程
,则方程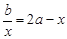 有实根的概率为( )
有实根的概率为( )A.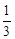 | B.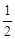 | C.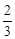 | D.1 |
科目:高中数学 来源:不详 题型:解答题
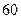 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段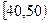 ,
,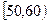 …
…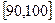 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: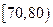 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;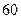 名学生中随机抽取
名学生中随机抽取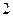 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记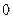 分,在
分,在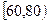 记
记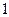 分,在
分,在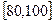 记
记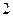 分,用
分,用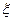 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求 的分布列和数学期望.
的分布列和数学期望.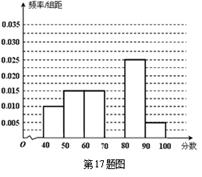
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 过第二
过第二 次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。
次烧制后,甲、乙、丙三件产品合格的概率依次为0.6,0.5,0.75。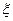 ,求随机变量
,求随机变量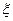 的期望。
的期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.12 | B.3 | C.18 | D.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为
进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为 、
、 、
、 、
、 ,且各
,且各 轮问题能否正确回答互不影响。
轮问题能否正确回答互不影响。 个数记为
个数记为 ,求随机变量
,求随机变量 的分布列和期望。
的分布列和期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com