
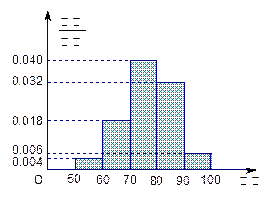
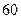 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段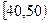 ,
,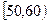 …
…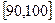 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: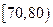 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;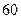 名学生中随机抽取
名学生中随机抽取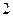 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记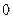 分,在
分,在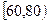 记
记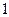 分,在
分,在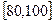 记
记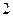 分,用
分,用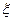 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求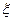 的分布列和数学期望.
的分布列和数学期望.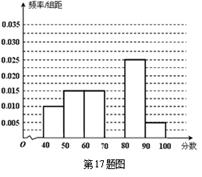
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
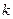 次成功,则第
次成功,则第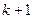 次也成功的概率为
次也成功的概率为 ,当第
,当第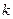 次失败,则第
次失败,则第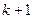 次成功的概率为
次成功的概率为 ,若首次试验成功和失败的概率都是
,若首次试验成功和失败的概率都是 ,求第
,求第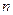 次试验成功的概率
次试验成功的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示方案
表示方案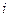 实施两年后柑桔产量达到灾前产量的倍数。
实施两年后柑桔产量达到灾前产量的倍数。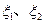 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
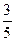 ,已知比赛中,俄罗斯女排先赢了第一局,求:
,已知比赛中,俄罗斯女排先赢了第一局,求: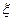 ,求
,求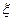 的分布列及
的分布列及 (均用分数作答).
(均用分数作答).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
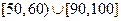 内的
内的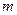 、
、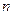 ,求事件“
,求事件“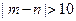 ”的概率
”的概率查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com