
 如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,
如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,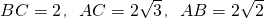 ,
,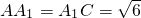 .
. ,AA1=A1C=
,AA1=A1C= ,∴AC2=AA12+A1C2,
,∴AC2=AA12+A1C2, ,AB=2
,AB=2 ,AC2=AB2+BC2,
,AC2=AB2+BC2,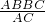 =
=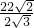 =
= ,EC=
,EC= =
=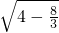 =
= ,
, -
- =
= ,
,
 ,0),A1(0,0,
,0),A1(0,0, ),B(
),B( ,
, ,0),C(0,
,0),C(0, ,0),
,0), =(0,
=(0, ,-
,- ),
), =(
=( ,
, ,0),
,0), ,
, >=
>=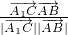 =
= ,
, .
. ,
, 的坐标,利用向量的夹角公式即可求得.
的坐标,利用向量的夹角公式即可求得.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=2
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.
如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
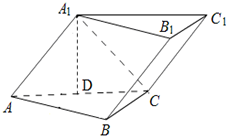 如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,BC=2,AC=2
如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,BC=2,AC=2| 3 |
| 2 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:
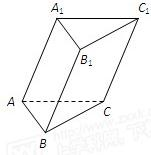 如图,已知斜三棱柱ABC-A1B1C1的底面边长分别是AB=AC=10cm,BC=12cm,侧棱AA1=13cm,顶点A1与下底面各个顶点的距离相等,求这个棱柱的全面积.
如图,已知斜三棱柱ABC-A1B1C1的底面边长分别是AB=AC=10cm,BC=12cm,侧棱AA1=13cm,顶点A1与下底面各个顶点的距离相等,求这个棱柱的全面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com