
【题目】已知函数 ![]() 的最小值为
的最小值为 ![]() .
.
(1)求 ![]() 的值;(2)求
的值;(2)求 ![]() 的解析式.
的解析式.
【答案】(1)-4;(2)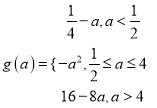
【解析】试题分析:(1)由a=2,求得f(t)=(t﹣2)2﹣4,即可得到最小值g(2);
(2)运用换元法和二次函数的对称轴和区间的关系,对a展开讨论,即可得到最小值的表达式.
试题解析:
(1)a=2时,f(x)=4x﹣42x(﹣1≤x≤2)
=(2x﹣2)2﹣4,
令t=2x(![]() ≤t≤4),
≤t≤4),
即有f(t)=(t﹣2)2﹣4,
由于2∈[![]() ,4],可得最小值g(2)=﹣4;
,4],可得最小值g(2)=﹣4;
(2)函数f(x)=4x﹣a2x+1(﹣1≤x≤2),
令t=2x(![]() ≤t≤4),
≤t≤4),
则f(t)=t2﹣2at=(t﹣a)2﹣a2,
当a≤![]() 时,区间[
时,区间[![]() ,4]为增区间,即有t=
,4]为增区间,即有t=![]() 取得最小值
取得最小值![]() ﹣a;
﹣a;
当![]() <a<4时,当t=a时,取得最小值﹣a2;
<a<4时,当t=a时,取得最小值﹣a2;
当a≥4时,区间[![]() ,4]为减区间,即有t=4取得最小值16﹣8a.
,4]为减区间,即有t=4取得最小值16﹣8a.
即有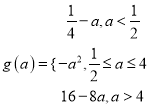 .
.


科目:高中数学 来源: 题型:
【题目】一次数学会议中,有五位教师来自![]() 三所学校,其中
三所学校,其中![]() 学校有
学校有![]() 位,
位,![]() 学校有
学校有![]() 位,
位,![]() 学校有
学校有![]() 位。现在五位老师排成一排照相,若要求来自同一学校的老师不相邻,则共有_______种不同的站队方法.
位。现在五位老师排成一排照相,若要求来自同一学校的老师不相邻,则共有_______种不同的站队方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:“若![]() ,则关于x的不等式
,则关于x的不等式![]() 的解集为空集”,那么它的逆命题,否命题,逆否命题,以及原命题中,假命题的个数是( )
的解集为空集”,那么它的逆命题,否命题,逆否命题,以及原命题中,假命题的个数是( )
A.0B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有两个命题:(1)不等式|x|+|x-1|>m的解集为R;(2)函数f(x)=(7-3m)x在R上是增函数;如果这两个命题中有且只有一个是真命题,则m的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将宽和长都分别为x,![]() 的两个矩形部分重叠放在一起后形成的正十字形面积为
的两个矩形部分重叠放在一起后形成的正十字形面积为![]() 注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形
注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形![]() ,
,

![]() 求y关于x的函数解析式;
求y关于x的函数解析式;
![]() 当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限集![]()
![]() ,如果
,如果![]() 中元素
中元素![]() 满足
满足![]() ,就称
,就称![]() 为“复活集”.
为“复活集”.
(1)判断集合 是否为“复活集”,并说明理由;
是否为“复活集”,并说明理由;
(2)若![]() ,
,![]() ,且
,且![]() 是“复活集”,求
是“复活集”,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求证:“复活集”
,求证:“复活集”![]() 有且只有一个,且
有且只有一个,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共11只,现在盒子上开一小孔,每次只能飞出1只昆虫(假设任意1只昆虫等可能地飞出).若有2只昆虫先后任意飞出(不考虑顺序),则飞出的是蝴蝶或蜻蜓的概率是![]() .
.
(1)求盒子中蜜蜂有几只;
(2)若从盒子中先后任意飞出3只昆虫(不考虑顺序),记飞出蜜蜂的只数为X,求随机变量X的分布列与数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com