
分析 (1)求得f(x)的导数,求得切线的斜率和切点,由切线的方程,可得f(1)=1+ln2,f′(1)=-($\frac{1}{2}$+ln2),解方程即可得到所求值;
(2)对于正整数k,函数g(x)=$\frac{k}{1+x}$,在区间(-1,+∞)上为减函数,于是对任意的正数c,f(c)=g(b)>g(c),当x>0时,不等式f(x)>g(x)?k<$\frac{(x+1)[1+ln(x+1)]}{x}$,令h(x)=$\frac{(x+1)[1+ln(x+1)]}{x}$,(x>0),利用导数研究其单调性,当x>0时,可得:h(x)的最小值∈(3,4).可得:正整数k≤3.再证明:当k=3时,对-1<x<0,有f(x)<g(x)即可.
解答 解:(1)函数f(x)=$\frac{1+μln(x+1)}{λx}$的导数为
f′(x)=$\frac{\frac{μ}{x+1}•λx-λ(1+μln(x+1))}{(λx)^{2}}$,
由题意可得f(1)=1+ln2,f′(1)=-($\frac{1}{2}$+ln2),
即为$\frac{1+μln2}{λ}$=1+ln2,$\frac{\frac{μ}{2}•λ-λ(1+μln2)}{{λ}^{2}}$=-$\frac{1}{2}$-ln2,
解得λ=μ=1;
(2)f(x)=$\frac{1+ln(x+1)}{x}$,
对于正整数k,函数g(x)=$\frac{k}{1+x}$在区间(-1,+∞)上为减函数,
于是对任意的正数c,f(c)=g(b)>g(c),
当x>0时,不等式f(x)>g(x)?k<$\frac{(x+1)[1+ln(x+1)]}{x}$,①,
令h(x)=$\frac{(x+1)[1+ln(x+1)]}{x}$(x>0),
则h′(x)=$\frac{x-1-ln(x+1)}{{x}^{2}}$.
再令φ(x)=x-1-ln(x+1)(x>0),
φ′(x)=$\frac{x}{x+1}$>0,故φ(x)在x>0时为增函数.
又φ(2)=1-ln3<0,φ(3)=2-ln4>0,
因此存在唯一的正实数x0使φ(x0)=x0-1-ln(x0+1)=0,②
h′(x)>0,此时h(x)为增函数.
因此,当x>0时,由②可得:h(x)的最小值为h(x0)=x0+1∈(3,4).
由①可得:正整数k≤3,③.
下面证明:当k=3时,对-1<x<0,有f(x)<g(x).④.
-1<x<0,有f(x)<g(x)?1-2x+(x+1)ln(x+1)>0.
令u(x)=1-2x+(x+1)ln(x+1),其中:-1<x<0,则u′(x)=ln(x+1)-1<0,
故u(x)在(-1,0)上为减函数,于是u(x)>u(0)>0,因此④成立.
而g(x)=$\frac{3}{x+1}$(x∈(-1,+∞))的值域为(0,+∞),
f(x)=$\frac{1+ln(1+x)}{x}$(x∈(0,+∞))的值域为(0,+∞),
f(x)=$\frac{1+ln(x+1)}{x}$(x∈(-1,0))的值域为R,
结合函数的图象可得:对任意的正数c,存在实数b满足-1<b<c,且f(c)=g(b).
综上可得:正整数k的最大值为3.
点评 本题考查了利用导数研究切线的斜率和函数的单调性极值与最值,考查了转化思想的运用,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$:1 | B. | 1:$\sqrt{2}$ | C. | $\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{3}$:$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
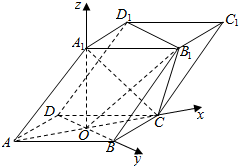 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.平面OCB1的法向量$\overrightarrow{n}$=(x,y,z)为( )| A. | (0,1,1) | B. | (1,-1,1) | C. | (0,1,-1) | D. | (-1,-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com