
【题目】朱世杰是历史上最伟大的数学家之一,他所著的![]() 四元玉鉴
四元玉鉴![]() 卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤
卷中“如像招数”五问有如下问题:“今有官司差夫一千八百六十四人筑堤![]() 只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”
只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”![]() 其大意为:“官府陆续派遣
其大意为:“官府陆续派遣![]() 人前往修筑堤坝,第一天派出
人前往修筑堤坝,第一天派出![]() 人,从第二天开始,每天派出的人数比前一天多
人,从第二天开始,每天派出的人数比前一天多![]() 人,修筑堤坝的每人每天分发大米
人,修筑堤坝的每人每天分发大米![]() 升,共发出大米
升,共发出大米![]() 升,问修筑堤坝多少天”
升,问修筑堤坝多少天”![]() 这个问题中,前
这个问题中,前![]() 天一共应发大米____________升.
天一共应发大米____________升.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
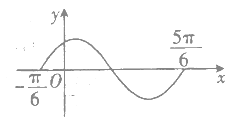
【题目】如图所示的是函数![]() (
(![]() ,
,![]() )在区间
)在区间![]() 上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移
上的图象,将该函数图象各点的横坐标缩小到原来的一半(纵坐标不变),再向右平移![]() (
(![]() )个单位长度后,所得到的图象关于直线
)个单位长度后,所得到的图象关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
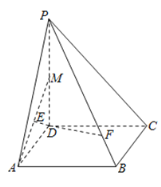
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 底面ABCD,且
底面ABCD,且![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.

(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
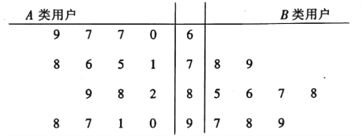
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
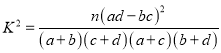 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上一点,且
上一点,且![]() 到
到![]() 的焦点的距离为
的焦点的距离为![]() .
.
(1)若直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,证明:
为坐标原点,证明:![]() ;
;
(2)若![]() 是
是![]() 上一动点,点
上一动点,点![]() 不在直线
不在直线![]() :
:![]() 上,过
上,过![]() 作直线垂直于
作直线垂直于![]() 轴且交
轴且交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .试判断
.试判断![]() 与
与![]() 中是否有一个为定值?若是,请指出哪一个为定值,并加以证明;若不是,请说明理由.
中是否有一个为定值?若是,请指出哪一个为定值,并加以证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有以下四个命题:
有以下四个命题:
①对于任意的![]() ,都有
,都有![]() ; ②函数
; ②函数![]() 是偶函数;
是偶函数;
③若![]() 为一个非零有理数,则
为一个非零有理数,则![]() 对任意
对任意![]() 恒成立;
恒成立;
④在![]() 图象上存在三个点
图象上存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.其中正确命题的序号是__________.
为等边三角形.其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图一是第1代“勾股树”,重复图一的作法,得到图二为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第n代“勾股树”所有正方形的面积的和为( )
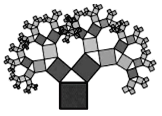
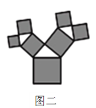
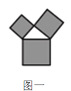
A. nB. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com